How to Calculate Covariance using Covariance Formula & Solved Examples?

In this article, you will learn what covariance and its formula are. You will also know what the difference between covariance and correlation is.

What is Covariance?

The covariance is the absolute relationship between two variables, x, and y. It measures the direction of the relationship between two variables regardless of their magnitude.

For example, suppose the covariance sign is positive. In that case, it means both variables are directly proportional to each other, i.e., the increase in x will result in the increase in y and vice versa. But when the sign is negative, it means that both variables move in the opposite direction, i.e., if one increases, the other decreases.

The concept of covariance is essential to discussing the relationship between two variables in economics. For example, in trading, positive covariance is needed for profit earning.

Covariance Formula

In statistics, the covariance of two random variables is used to measure the relationship between them. The formula of covariance between x and y is:

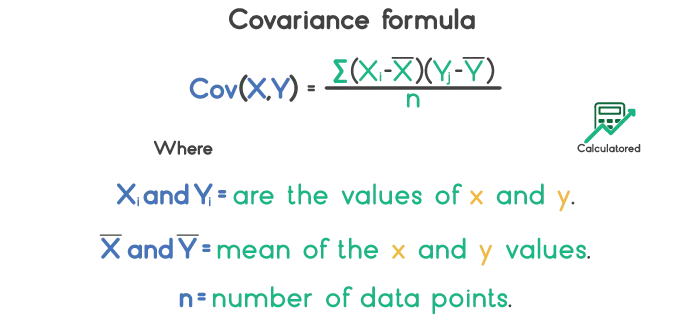
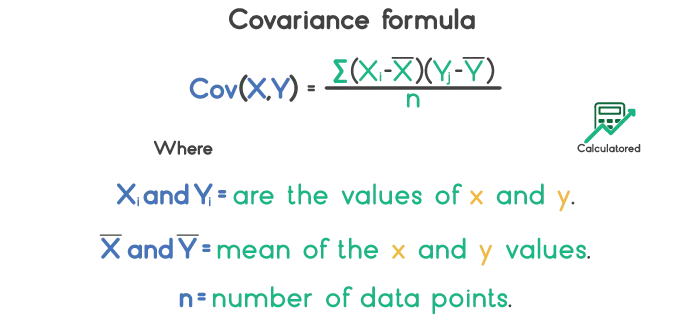
For example, if X has the values 2, 5, 6, 8, 9 and Y has the values 4, 3, 7, 5, 6. We have to calculate the covariance between them.

Here,

$$ \bar X \;=\; \frac{\sum X_i}{n}\;=\; \frac{2+5+6+8+9}{5} \;=\;\frac {30}{5} \;=\;6 $$

And,

$$ \bar Y \;=\; \frac{\sum Y_i}{n}\;=\; \frac{4+7+5+6+3}{5} \;=\;\frac {25}{5} \;=\;5 $$

Now by using the covariance formula, we can get the value of covariance between X and Y, that is:

$$ Cov(X,Y) \;=\; \frac{\sum (X_i - \bar X) (Y_j - \bar Y)}{n} \;=\; 1.8 $$

How to Calculate Covariance Between Two Variables?

Let X_i has the values {x₁, x₂, x_3,x₄,...} and Y_j has the values{y₁, y₂, y₃,...}. X̄ and Ȳ are the mean of x and y values. Then the covariance between X and Y can be calculated by using the following formula:

$$ Cov(X,Y)\;=\; \frac{\sum (X_i- \bar X) (Y_j - \bar Y)}{n} $$

Where n is the number of data values.

Let’s see the following examples to understand how covariance is calculated.

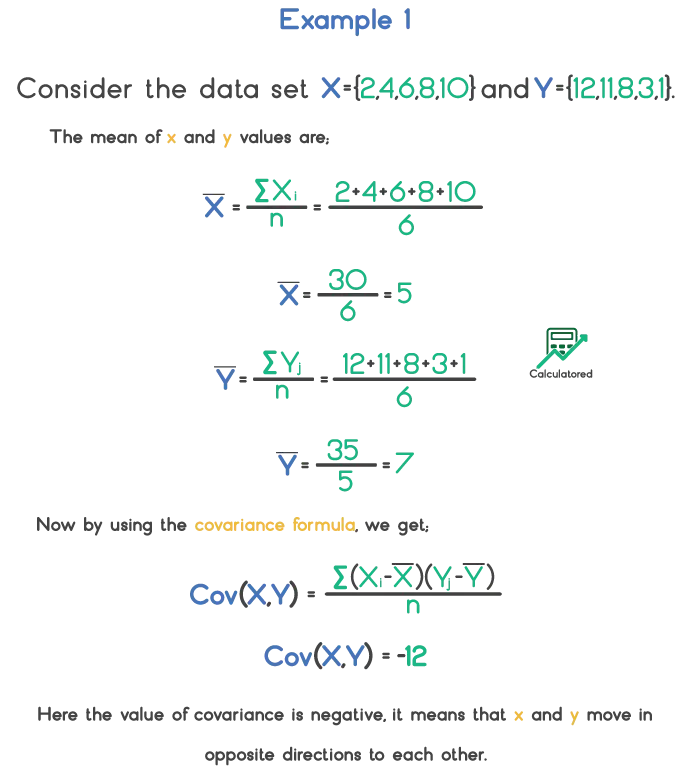
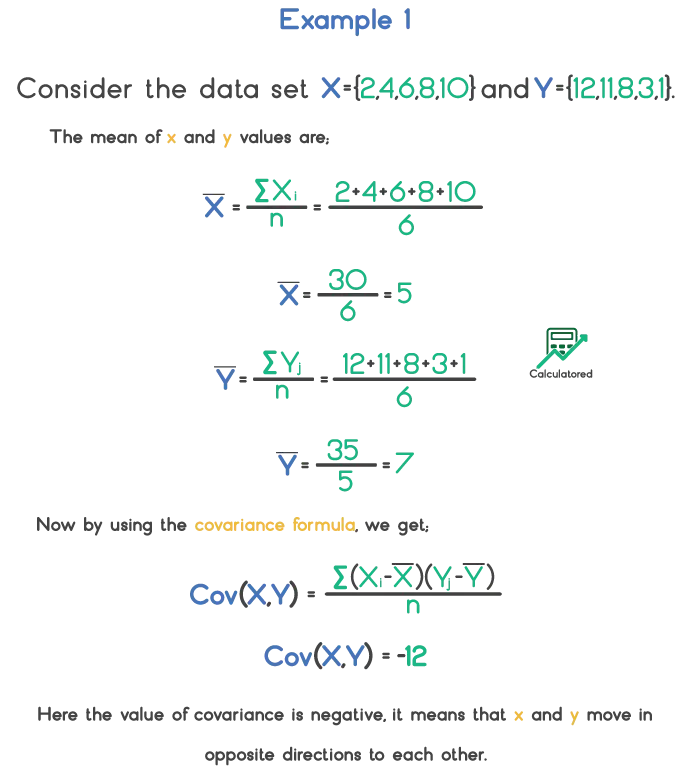
Here, the value of covariance is positive which means that both variables move in the same direction.

Covariance and Correlation

The covariance and correlation both are statistical terms. Both explain the relationship between two random variables. Covariance tells you how these variables differ by measuring the directional variation, whereas the correlation suggests how the two random variables are related.

Covariance Formula for a Sample Data

The covariance for sample data explains the reliability of the sample means as estimators. The covariance formula for a sample data in statistics is:

$$ Cov(X,Y)\;=\; \frac{\sum (X_i - \bar X) (Y_j - \bar Y)}{n-1} $$

X_i= values of x,
Y_i= values of y,
X̄= mean of the x values.
Ȳ = mean of the y values.
n = number of data points.

FAQ’s on Covariance Formula

Is Cov (X,Y) the same as Cov (Y,X)?

Yes, both are same because covariance of two variables has symmetrical properties. So,

$$ Cov(X,Y) \;=\; Cov(Y,X) $$

What is the Formula of Calculating Covariance?

The formula of covariance between two variables is:

$$ Cov(X,Y)\;=\; \frac{\sum (X_i - \bar X) (Y_j - \bar Y)}{n} $$

X_i = values of x,

Y_is = values of y,

X̄ = mean of the x values.

Ȳ= mean of the y values.

n = number of data points.