Understand slope formula and Derivation? How to Find Slope with Two Points, Graphs and Equations

In this article, you will learn what is the slope of a line and its formula. You will also learn what are 3 slope formulas.

What is Slope?

The slope is a geometric term that explains the inclination and steepness of a line. It tells how steep a line is and how quickly it increases or decreases. It is an useful idea in mathematics that finds the behaviour of straight lines. In a two-dimensional plane, the slope of a line is the ratio of differences along the x and y-axis.

It is a numerical measure of a line’s inclination and steepness with respect to horizontal and vertical axis. It is an important factor in geometry as well as in calculus.

Slope Formula

As it is clear by the definition that the slope of line is the ratio of vertical and horizontal distance. So for a line y=mx+c, the general formula of slope is:

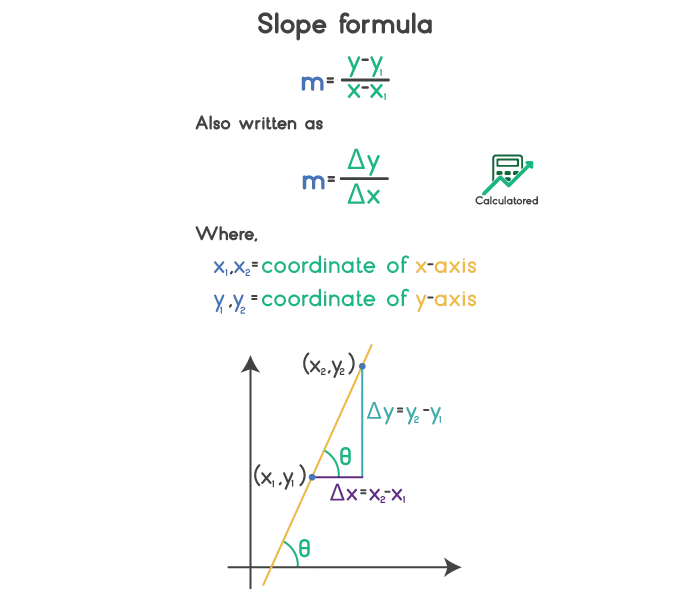
It helps to find an equation of a straight line. Here the slope is denoted by ‘m’.

Since the slope is the rate of change in vertical and horizontal coordinates, the formula can also be written as:

$$ m \;=\; \frac{\Delta y}{\Delta x} $$

Derivation of Slope Formula

Consider the equation of line,

$$ y \;=\; ax \;+\; b $$

Suppose, (x₁,y₁) and (x₂,y₂) are two points on the line so,

$$ y_1 \;=\; ax_1 \;+\; b $$

and

$$ y_2 \;=\; ax_2 \;+\; b $$

By simplifying the above equations for a, we get,

$$ a \;=\; \frac{y_2-y_1}{x_2-x_1} $$

Which is the equation of slope of the line y = ax + b.

How to Find the Slope of a Line?

Suppose, a line is formed by joining two point A and B having coordinates (x₁,y₁) and (x₂,y₂) then the slope of line AB can be calculated as:

$$ m \;=\; \frac{y_2-y_1}{x_2-x_1} $$

Here we provide you a step-by-step method to find the slope of a line. Use the following steps to find slope of a line:

Find the change in vertical coordinates of the line.
Find the change in horizontal coordinates.
Substitute the values of change in vertical and horizontal coordinates in the slope formula, m = y₂-y₁/x₂-x₁
Simplify the ratio to get the exact slope.

Let’s understand how to find the slope of a line by discussing slope formula examples.

How to Find Slope on a Graph?

It is another method of finding slope of line from a graph. You can calculate the slope from a graph by using the following steps.

Draw a line with random points on the graph.
Label the point as A and B.
Now calculate the rise from A to B vertically. Remembering the positive sign indicates upward direction and negative indicates downward direction.
Now calculate the run from A to B which is the horizontal distance between them.
Now use the divide the vertical distance (rise) by the horizontal distance (run) between them as, $$ m \;=\; \frac{rise}{run} $$

Slope Formula Examples

Related Formulas

In geometry, there are three major slope formulas. These are:

Slope-intercept Formula:
y = mx + c
Point slope Formula:
y-y₁=m(x-x₁)
Standard Form Formula:
Ax + By = C

FAQ’s on Slope Formula

What is the Two Point Slope Formula?

Suppose, a line is formed by joining two point A and B having coordinates (x₁,y₁) and (x₂,y₂) then the two point slope of line AB can be calculated as: