Understand the Absolute Value Formulas & Rules to Solve the Absolute Value Equations
Introduction
In this article, you will learn what absolute value inequality is and how to solve absolute value inequalities. Also understand the absolute value equation rules.
Absolute Value Definition
An algebraic expression, containing inequality symbols, is called an absolute value inequality. It is a simple linear equation that follows the rules of absolute numbers. There are four types of inequality symbols in this expression of absolute value definition. These are >,<,≤, ≥.
Absolute Value Formulas
This formula contains an absolute value equation. It is a way of writing an inequality in algebraic expression. The absolute value equation formula is generally expressed as:
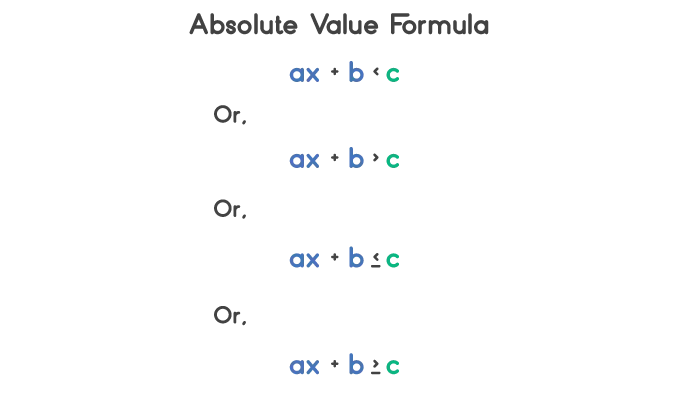
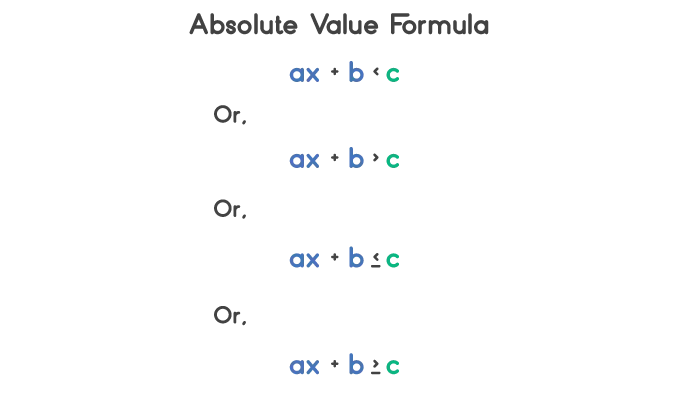
Absolute Value Equation Rules
To solve the absolute value inequality equations, remember the following rules to express the solution of a given equation. These are:
- When the inequality is in the form of |x| < a or |x| < a
- When the inequality is in the form of |x| > a or |x| > a
- When the inequality is in the form of |x| < - a or |x| < - a
- When the inequality is in the form of |x| > - a or |x| > - a
In this case,
If
|x| < a -a < x < a
And if
|x| < a -a < x < a
If
|x|> a x < -a or x > a
And if
|x| > a x < -a or x > a.
Since the absolute value always results in a positive value. But when the value of x is less than or equal to -a. It means that there will be no solution for x.
Here, in this case, the value of x is greater than or equal to –a, so the solution of x will be all real numbers.
How to Solve an Equation with Absolute Value?
The absolute value equation rules are essential to solving these inequalities. Here we provide a step-by-step way of solving absolute value inequalities.
- First, remember that the inequality has to be solved for the values of the variables involved.
- Isolate the absolute value on one side and the remaining values on the right side.
- Write the equation in compound inequality by using inequality signs.
- Find the values of the variable x and graph the solution on a real line.
- Here are some examples to understand how to solve the absolute value equation.
Example of Absolute Value Equation


Formulas Related to Absolute Value Equation Formula
- Absolute value
- Double absolute value inequalities
The absolute value formula for a number c is,
c = c c ≥ 0 -c c< 0
The double absolute value inequalities can be expressed in general form as,
ax + b + c < d
It can be expressed using all four inequality symbols like >,<,≤, ≥.
FAQ’s
What is the absolute value of -3?
By the definition of absolute value,
|-3|=3
Because the number 3 is greater than zero. It does not matter the negative sign because the absolute value formula always gives a positive number.
What is the absolute value equation?
It is an algebraic expression with inequality symbols. The general form of absolute value inequality is:
ax + b < c
Or,
ax + b > c
Or,
ax + b ≤ c
Or,
ax + b ≥ c
What is the Absolute Value of -5?
The absolute value of -5 is 5. It is because by the definition of absolute value,
|-5|=5


