What is the Mean Formula? How to Calculate Mean with Examples?

In this article, you will learn about the mean and its formula. You will also learn how the mean is calculated.

What is Mean?

The mean is an essential concept in mathematics and statistics. It refers to the average of all numbers of a data set. It is calculated by adding the numbers and dividing by the total number of values. There are different mean formulas in mathematics, such as arithmetic mean, geometric mean, harmonic mean, root mean square and contraharmonic mean.

Mean in Statistics

In statistics, the mean is the major concept that summarizes the data by a single value. The mean formula varies according to grouped and ungrouped data. There are three measures of central tendency: mean, median and mode.

Mean Formula

Generally the mean is calculated by dividing the sum of all values to the total number of values. The mean formula is given by:

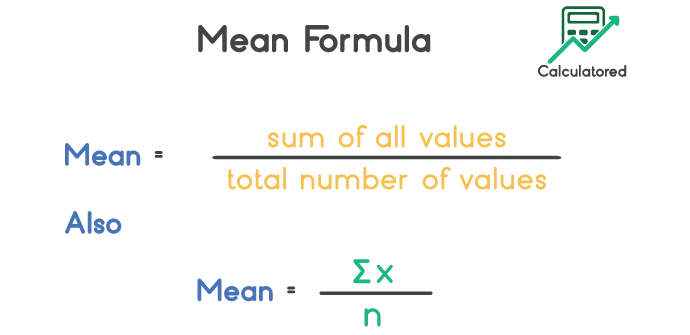
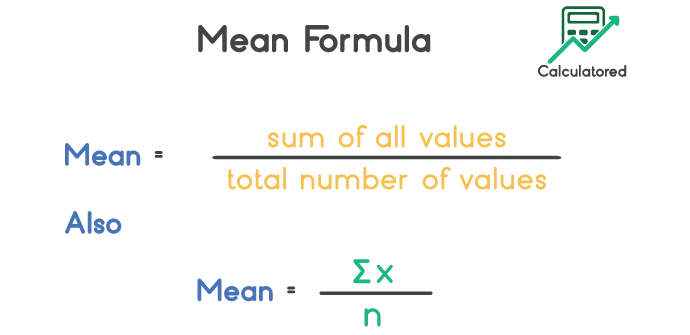
How do you Calculate the Mean?

Suppose a set of date x_n = x₁, x₂, x₃,…… x_n , with n number of values. We can calculate mean of this arithmetic sequence of data by using mean formula which is:

$$ Mean \;=\; \frac{Sum \; of \; all \; values}{Total \; number \; of \; values} $$

Here we have,

$$ Mean \;=\; {x_1+x_2+x_3+...+x_n}{n} $$

In more generalized form,

$$ Mean \;=\; \frac{\sum X_n}{n} $$

Let’s see the following examples to understand how the mean is calculated.

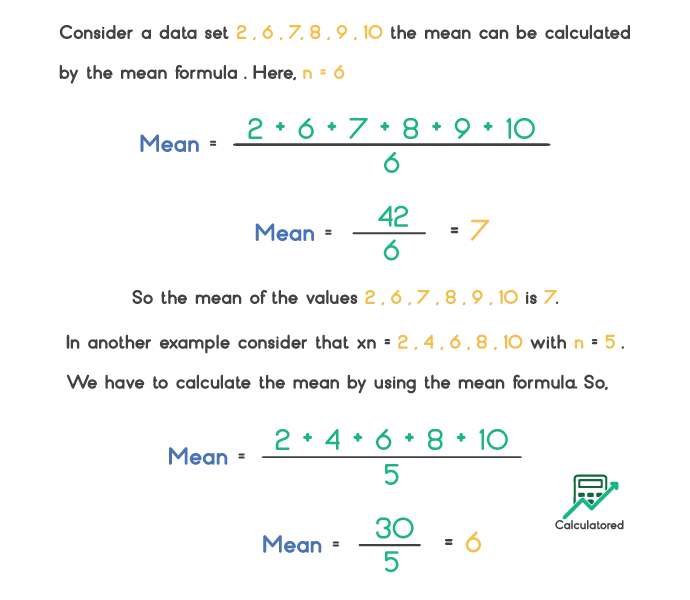
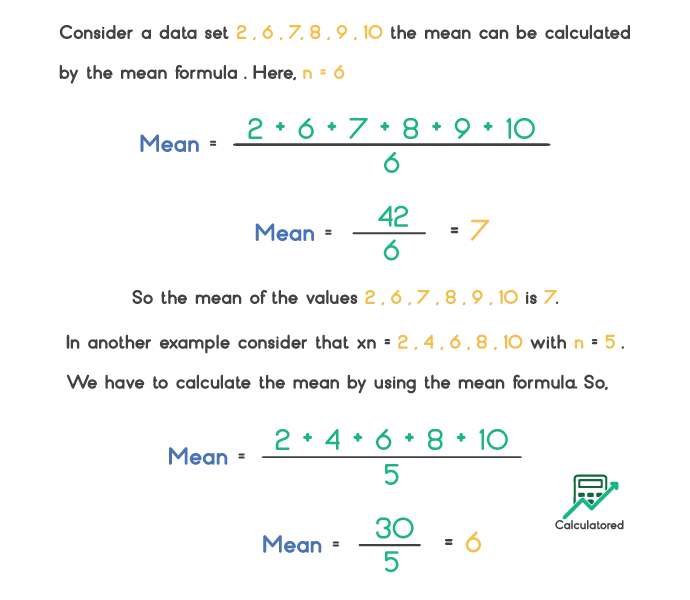
So this is the manual and practical calculation of mean. Calculating the mean is a quite simple and easy to understand concept of statistics. But the mean calculator with solution is a great alternative to skip arrangments of data, sum of this data and taking the average at the end.

Mean, Median and Mode Formula in Statistics

In statistics, for x_n=x₁, x₂, x₃,…… x_n values the mean can be calculated by the formula,

$$ Mean \;=\; \frac{\sum X_n}{n} $$

Here,
X_n = sum of all observations.
n = total number of observations.

But sometimes while calculating the mean there is a deviaton occurs. The standard value of mean occurs above or below to the exact value which is known as z score. We may calculate standard score of any data set by using the z score formula.

Median

The median of a data set can be calculated by ordering the number from smallest to largest and selecting the middle value. If there are two values in the middle, then median is the mean of those two values.

For example, in data set 1, 5, 4, 5, 3, 7, 2, 8. Ordering it from small to large value 1, 2, 3, 4, 5, 5, 7 there are two values in the middle so calculating the mean of 4 and 5, the median of this set of data is 4.5.

Mode

The mode is the frequently appearing value in the data set. A data set can have more than one mode.

For example in data set 1, 1, 5, 4, 5, 9, 1, the mode is 1 because it is appearing three times.

Types of Mean

There are four types of mean in math. These are:

• Arithmetic mean
• Geometric mean
• Harmonic mean
• Contraharmonic mean

Arithmetic Mean

The arithmetic mean is the ratio of all observations to the total number of observations in a sample data. In statistics, it refers to the average of the observations. The arithmetic mean formula can be written as:

$$ Mean \;=\; \frac{\sum f_i}{N} $$

Where X is the mean value of the given data set, f is the frequency of the individual data and N is the sum of all frequencies.

Geometric Mean

The geometric mean is defined as the nth root of the product of n numbers in the given sample data. The formula to find the geometric mean for a data set is:

$$ G.M \;=\; \sqrt{x_1 \cdot x_2 \cdot x_3...\cdot x_n} $$

Harmonic Mean

The harmonic mean is defined as the reciprocal of the arithmetic mean of the reciprocal data set. The formula to calculate harmonic mean is given by:

$$ H.M \;=\; \frac{1}{\frac{ \sum \frac{1}{x_i}}{N}} $$

It can be written as:

$$ H.M \;=\; \frac{N}{\sum \biggr( \frac{1}{x_i} \biggr) } $$

Contraharmonic Mean

The contraharmonic mean is a statistical term that can be found by the ratio of the sum of squares of all values by the sum of all values. The formula of contraharmonic mean can be written as:

$$ C.M \;=\; \frac{ \sum (x_n)^2}{\sum (x_n)} $$

Where,

Σ(x_n)² = The sum of square of all x_n = x₁, x₂, x₃,…… x_n

Σ(x_n) = The sum of all x_n = x₁, x₂, x₃,…… x_n

FAQ's on Mean Formula

What is the Easiest Way to Find the Mean?

The easiest way to find the mean is by adding all numbers and dividing it by the total number of values.

What is the Formula for Calculating Mean?

The formula to calculate mean is:

$$ Mean \;=\; \frac{Sum \; of \; all \; values}{Total \; number \; of \; values} $$