Easiest way to Solve Arithmetic Sequence with Arithmetic Sequence Formula
In this article, you will learn what an arithmetic sequence is. You will also learn how to find the nth term and sum of the consecutive terms of the sequence.
What is Arithmetic Sequence?
A sequence is a continuous ordered set of different objects, events or things having a particular difference. In mathematics arithmetic sequence is a sequence of numbers whose common difference remains the same.
In an arithmetic sequence, every term can be obtained by adding or subtracting a fixed common difference. For example 2, 4, 6, 8… is an arithmetic sequence whose common difference is 2. It means the whole sequence can be obtained by adding 2 in the previous term.
Arithmetic Sequence Formula
There are three formulas of arithmetic sequence. One is for the nth term of the sequence; second one is for the sum of the n terms and third is to find common differences.
If a sequence has an=a1,a2,a3,...,an terms with n number of terms and the common difference is d, then the arithmetic sequence formula can be written as:


The formula to find the common difference between two consecutive terms is:
d = an - an-1
Let’s see the tutorial example to find the nth term and the sum of the n terms of a sequence.
Let 1, 3, 5, 7, 9, 11 ….be a sequence with n=8. Let’s find the 8th term of the sequence and sum of the first 10 terms.
Here we know n=8, the common difference will be calculated as;
d = a2-a1
d = 3-1 = 2
It means that every term can be calculated by adding 2 in the previous term. Now by using arithmetic sequence formula,
an = a1+(n-1)d
We have to calculate a8
a8 = 1+(8-1)(2)
a8 = 1+(7)(2) = 15
So a8 = 15
Now to find the sum of the first 10 terms we will use the following formula.
$$ S_n \;=\; \frac{n}{2}[2a_1+(n-1)×d] $$Substituting a1 = 1, n = 10 and d = 2
$$ S_{10} \;=\; \frac{10}{2}[2(1)+(10-1)×2] $$Simplifying it,
$$ S_{10} \;=\; \frac{10}{2} [2+(9)×2] \;=\; 5(2+18) $$ $$ S_{10} \;=\; 5×20 \;=\; 100 $$So the sum of the first 10 terms is 100.
How do you Derive the Arithmetic Sequence Formula?
Let a sequence has n number of terms and the terms are an=a1,a2,a3,...,an-1,an the common difference d between every consecutive term is d =an-an-1
Since we know that every term of the sequence can be obtained by adding the common difference then all terms of the sequence can be written in the form of;
an = a1,a1+d,a1+2d,...,a1+(n-1)d
So, summarizing above equation
an = a1+(n-1)d
How to Solve Arithmetic Sequence Equations?
Let a sequence has n number of terms and the terms are an=a1,a2,a3,...an-1,an and d is the common difference between every term of the sequence. The nth term of the sequence can be calculated as:
an = a1+(n-1)d
Let’s see the following example to learn how to calculate the nth term of a sequence.


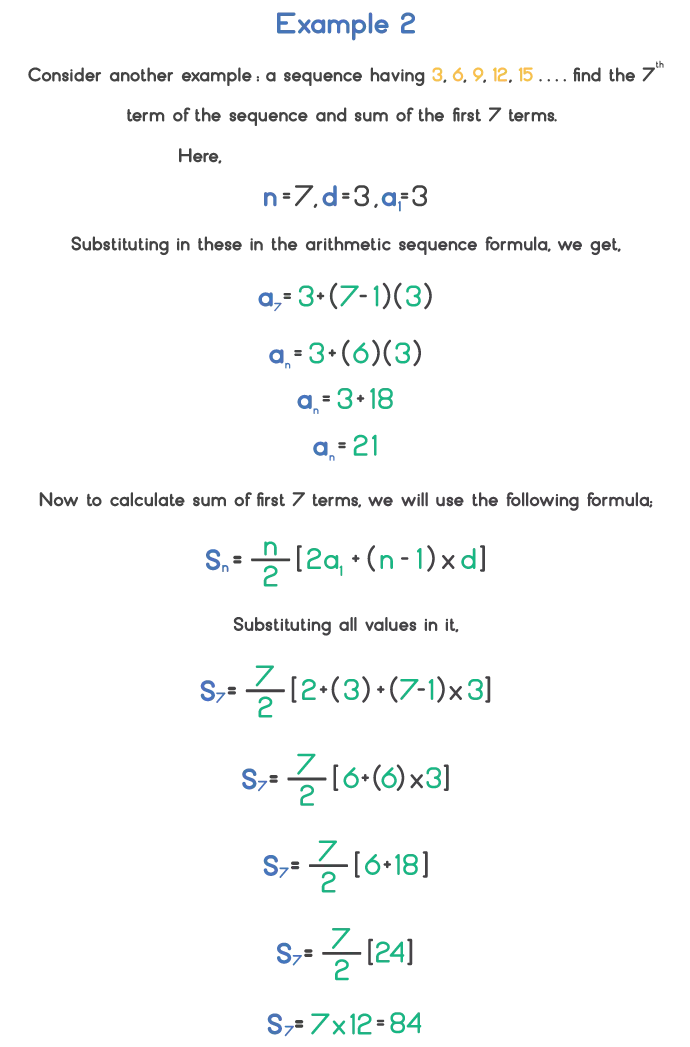
Related Formulas
- Arithmetic Mean Formula
- Geometric Sequence Formula
- Harmonic Mean Formula
Arithmetic Mean Formula
The concept of arithmetic mean is basically the average of numbers. But the method of its calculatiom may vary on the basis of frequency of numbers in a data set. The general formula to calculate arithmetic mean of a data set is:
$$ \sum \frac{ \bar X}{n} $$Geometric Sequence Formula
The geometric sequence of series of data is the sequence that have constant ratio of any two consecutive numbers. The geometric sequence formula to calculate this type of sequence is:
$$ a_n \;=\; ar^{n-1} $$Harmonic Mean Formula
The harmonic mean is the reciprocal of arithmetic mean. It is an average that we may calculate taking the reciprocal of every number in the series of dataset. The harmonic mean formula is given as:
$$ H.M \;=\; \frac{N}{\sum \biggr( \frac{1}{x_i} \biggr) } $$FAQ’s
What is an Arithmetic Sequence?
The arithmetic sequence is an ordered set of numbers having fixed common difference in every consecutive term of the sequence.
What is the Recursive Formula for Arithmetic Sequence?
The formula to calculate nth term of a sequence is;
$$ a_n\;=\;a_1+(n-1)d $$Where (an) an is the nth term, (a1) is the first term of the sequence and d is the common difference.
What is the formula to calculate the sum of n terms of the sequence?
The sum of n terms of the sequence is used to calculate the sum of all terms up to nth term. The formula is:
$$ S_n\;=\; \frac{n}{2}[2a_1+(n-1)×d] $$

