How to Find Midpoint using Midpoint Formula and Examples?

In this article, you will learn about midpoint and its formula. You will also learn how to calculate the midpoint of two numbers.

What is the Midpoint?

A midpoint is a middle point of the line segment formed by joining two points. It is a point which has equal distance from the two reference points of a line. It is the simplest concept in geometry.

For example a line formed by two points J and K. There will be a point M in the middle of both point J and K.

The point M has equal distance from J and K as shown in figure.

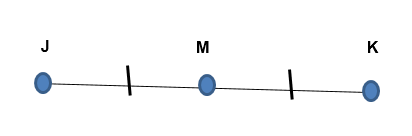
The midpoint of a line segment can also be defined as the average of the x-coordinates and y-coordinates of the end points of the line segment.

Midpoint Formula

The midpoint of a line divides it in two equal parts. The midpoint formula for two points X and Y can be written as:

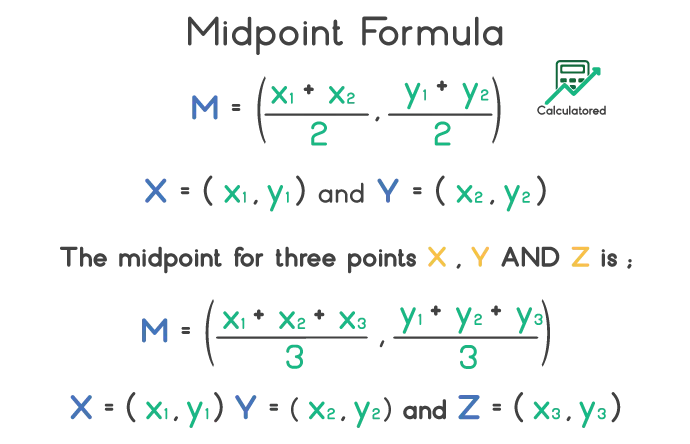
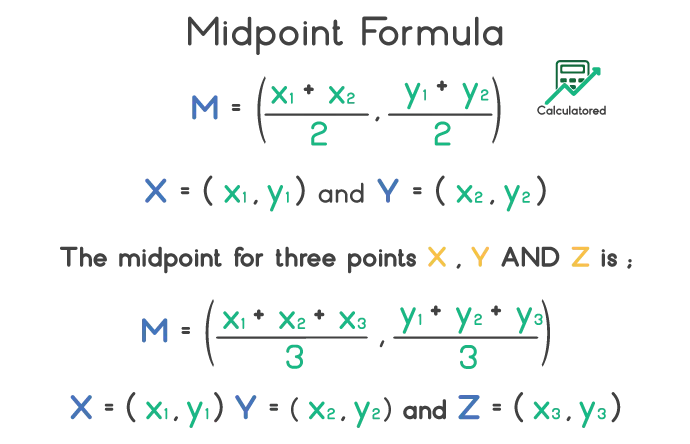
The formula to find midpoint between three points is also known as the centroid of a triangle formula.

Distance Formula and Midpoint Formula

Distance and midpoint formula are basic and important concepts of geometry. The distance formula is used to calculate distance between two points of a line. The distance formula for two points X and Y is:

$$ |XY| \;=\; \sqrt{(x_2-x_1)^2 \;+\; (y_2-y_1)^2} $$

Where,
X=(x₁,y₁) and Y=(x₂,y₂)

The midpoint formula is used to find the central point of a line segment form by two points. It is given as:

$$ M \;=\; \frac{x_1+x_2}{2} \;,\; \frac{y_1+y_2}{2} $$

How to Find the Midpoint?

The midpoint of a line can be calculated by using its end points in the midpoint formula geometry. Consider two end points X and Y of a line having coordinates (x₁,y₁) and (x₂,y₂) respectively. The midpoint between X and Y can be calculated as:

$$ M \;=\; \frac{x_1+x_2}{2} \;,\; \frac{y_1+y_2}{2} $$

Let’s see the following examples to understand how to calculate midpoint between two points.

Midpoint Formula Examples:

Formulas Related to Midpoint

There are two other formulas related to midpoint. These are:

1. Centroid of Triangle Formula
2. Section Formula

Centroid of Triangle Formula

The centroid of a triangle is the central point of it. The formula to find midpoint of a centroid of triangle is given as:

$$ M \;=\; \frac{x_1+x_2+x_3}{3} \;,\; \frac{y_1+y_2+y_3}{3} $$

Where X, Y and Z are the points of the triangle.

Section Formula

The section formula is used to find the coordinates of a point that divides a line. The section formula is:

$$ Section \;=\; \frac{mx_1+mx_2}{m+n} \;,\; \frac{my_1+my_2}{m+n} $$

Where m and n are the ratio points by which the line is divided.

Besides to midpoint formula, there are numbers of other concepts in geometry that you can learn here like trapezoid area formula, pythagorean formula, arc length formula and many more like that.

FAQ’s

What is the Midpoint Formula?

The midpoint of a line divides it in two equal parts. The midpoint formula for two points X and Y can be written as:

$$ M \;=\; \frac{x_1+x_2}{2} \;,\; \frac{y_1+y_2}{2} $$

Where X=(x1,y1) and Y=(x2,y2)

What does Midpoint mean?

The midpoint is a point on a line segment that has equal distance from the end points of the line.