Midpoint Calculator

The midpoint is the point at the same distance between 2 ends of a line. The midpoint calculator helps you to find the equidistance from two specified endpoints on a line by taking two coordinates in the cartesian coordinate system, with endpoints as A and B.

What Is the Midpoint?

A particular point that lies at the center of a line segment is known as the midpoint.

The midpoint divides the line segment into two parts of the same length. It lies in between two reference points that make up a line.

Midpoint Formula:

$$ (x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2} , \dfrac {y_{1} + y_{2}} {2}\right) $$

Where:

(x1, y1) _ First endpoint of a line segment
(x2, y2) _ Second endpoint of a line segment

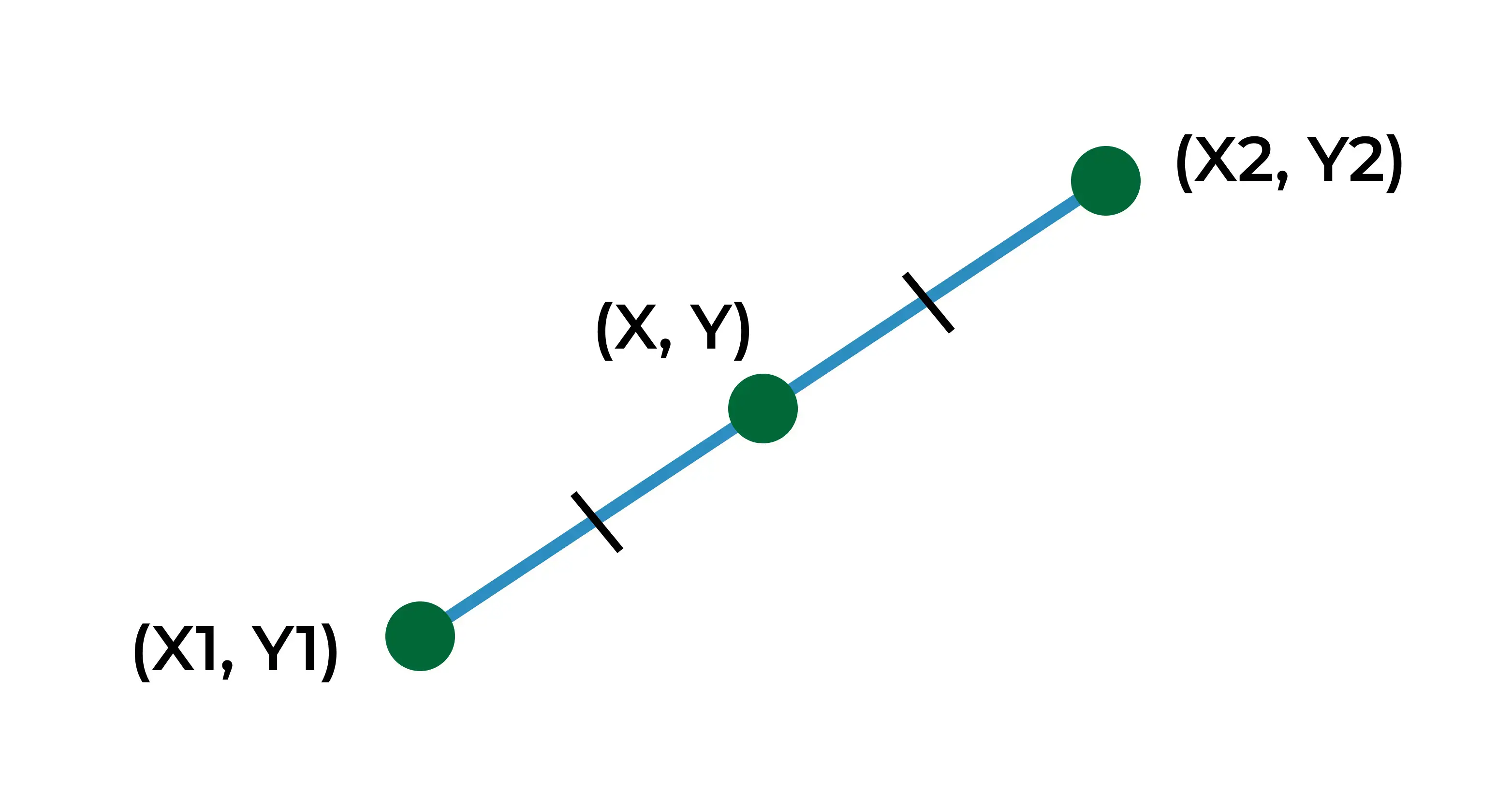
How To Find the Midpoint Between Two Points?

When you are given any two points of a bar, you can find the midpoint by hand.

• Add the X coordinate values and determine their half (Divide by 2)
• Repeat the same procedure for the Y coordinate of the midpoint

How To Find the Midpoint With Two Endpoints?

By using the endpoints evaluate the midpoint by following the steps below:

Step # 1: Consider the midpoint formula

$$ M = \left(\dfrac{x_1 + x_2}{2}, \; \dfrac{y_1 + y_2}{2}\right) $$

Step # 2: Separate the equations for both X and Y coordinates

$$ x_{M} = \dfrac {x_{1} + x_{2}} {2} $$

$$ y_{M} = \dfrac {y_{1} + y_{2}} {2} $$

Step # 3: Rearrange both equations to solve for X and Y 

$$ x_{2} = 2x_{M} - x_{1} $$

$$ y_{2} = 2y_{M} - y_{1} $$

Practical Example:

Let’s make a supposition that you have two endpoints A and B. So, calculate the midpoint of a line given 2 endpoints. These points have the coordinates as follows:

$$ A = \left(2, 8\right) $$

$$ B = \left(3, 6\right) $$

Solution:

$$ M = (x_M, \; y_M) $$

$$ M = \left(\dfrac{x_1 + x_2}{2}, \; \dfrac{y_1 + y_2}{2}\right) $$

$$ M = \left(\dfrac{2 + 3}{2}, \; \dfrac{8 + 6}{2}\right) $$

$$ M = \left(\dfrac{5}{2}, \; \dfrac{14}{2}\right) $$

$$ M = \left(2\dfrac{1}{2}, \; 7\right) $$

$$ M = (2.5, \; 7) $$

Instructions For Using This Calculator:

The midpoint calculator allows you to calculate the midpoint of the line segment by using the following guide:

Input Values:

• Enter the X coordinates and Y coordinates using numbers, fractions, mixed numbers, or decimals
• Tap on "Calculate"  

Output Summary:

• Midpoint of a line segment with stepwise calculations
• Decimal approximation, difference, and ratio
• Percent increase and arithmetic comparison
• Number line and Pie chart
• Vector length with possible intermediate steps
• Angles between vector and coordinate axes
• Polar coordinates

How to Find The Distance Between Two Points?

To discover the point that lies exactly between 2 coordinates, use the distance and midpoint calculator. This helps you to determine the distance between 2 points on a horizontal or vertical line.

The following formula can be used to calculate the distance between two endpoints of a line segment:

$$ d = \sqrt {(x_{2} - x_{1})^2 + (y_{2} - y_{1})^2} $$

• Determine the coordinates of both points 
• Put these coordinate values into the distance formula
• Find the square root after simplifying the expressions

Additional Queries:

How To Find the Midpoint of a Triangle?

The midpoint of the triangle is known as Centroid and can be calculated as:

• Determine the midpoints of all 3 sides
• Using the endpoint and midpoint of all sides, sketch bars that intersect the triangle sides from the center
• Where the edges meet, that is the midpoint of the triangle

What Is The Midpoint of (0,2) and (2,8)?

The midpoint between (0, 2) and (2, 8) is;

= (1, 5)

Do You Round Midpoints?

The midpoint can not be rounded off. 

References:

Wikipedia: Midpoint, Construction, Geometric properties involving midpoints, Generalizations

Khan Academy: Midpoint formula, Distance between points

Lumen Learning: Calculating Price Elasticities Using the Midpoint Formula, Midpoint Method, Distance Formula, The Standard Form Of Equations Of Circles