Best way to Understand the Limit Formula, Properties and Examples
In this article, you will learn what the limit of a function is and how it is calculated.
What is Limit?
If y=f(x) is a function, for point x=a if f(x) takes some intermediate form then we can consider the values of the function that are near to a. when these values approach to some definite unique number as x approaches to a then the resulting number is called the limit of f(x) at x=a.
The limit is the most fundamental and important concept in calculus. It helps to find the values of a function at some point that may not be determined by any other method.
Limit Formula
If y=f(x) is a function and the values of the function tend to some definite values when x approaches to a then the mathematically representation of limit of the function can be expressed as:


The formula of limit is read as the limit of f(x) is equal to L when x approaches to a.
Limit Properties
The properties of limit are:
Sum:
$$ \lim\limits_{x \to a} [f(x) \;+\; g(x)] \;=\; L \;+\; K $$
According to the sum property of limits, the sum of limits of two functions is equal to the limit of their sum.
Constant multiple:
$$ \lim\limits_{x \to a}[bf(x)] \;=\; bL $$
Product:
$$ \lim\limits_{x \to a} [f(x) \cdot g(x)] \;=\; L \cdot K $$
Quotient:
$$ \lim\limits_{x \to a} \frac{f(x)}{g(x)} \;=\; \frac{L}{K} $$
Power Rule:
$$ \lim\limits_{x \to a}[f(x)]^n \;=\; L^n $$
How to Find the Limit of a Function?
If y=f(x) is a function and the values of the function tend to some definite values when x approaches to a then the limit of function can be calculated by substitution of limit value in the function.
$$ \lim\limits_{x \to a}[f(x)] \;=\; L $$
See the below limits examples to understand how to evaluate limits.
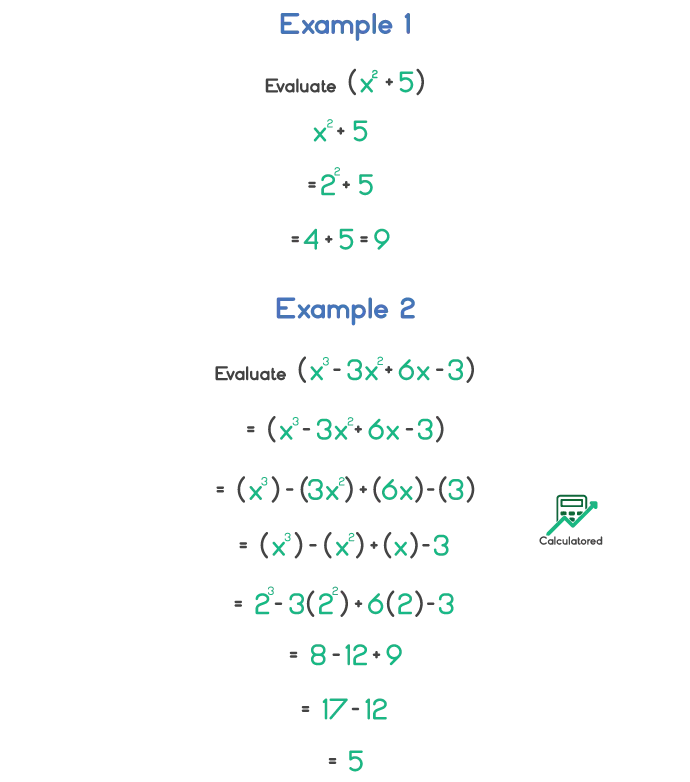

Limit Formulas
There are some important formulas of limits that are necessary to solve limits of any kind of function. These formulas are:
$$ \lim\limits_{x \to 0} e^x \;=\; 1 $$ $$ \lim\limits_{x \to 0} \frac{e^x-1}{x} \;=\; 1 $$ $$ \lim\limits_{x \to 0} \frac{a^x-1}{x} \;=\; log_e a $$ $$ \lim\limits_{x \to 0} \frac{log(1+x)}{x} \;=\; 1 $$ $$ \lim\limits_{x \to ∞} \left( 1 \;+\; \frac{1}{x} \right)^x \;=\; e $$ $$ \lim\limits_{x \to 0} \left( 1 \;+\; x \right)^{\frac{1}{x}} \;=\; e $$ $$ \lim\limits_{x \to ∞} \left( 1 \;+\; \frac{a}{x} \right)^x \;=\; e^a $$
Related Formula:
For instantaneous rate of change, the derivative formula will:
- Integral Formula
- $$ f(x) \;=\; \int_a^b g(x) dx $$
where
dx = infinitesimal displacement along x from a to b
g(x) = integrand function - Derivative Formula
- $$ \lim limits_(x to 0) \frac{δy}{δx} \;=\; \frac {f(x+δx)-f(x)}{(δx)} $$
where
δy = change in y
δx = change in x
FAQ’s
When does a Limit of a Function not Exist?
The limit of function exists only when the right and left hand side limit exist. If one of them does not exist then the limit of a function does not exist.
How to Find a One-Sided Limit?
The one-sided limit is the value of the function when x approaches the limit from one side only. Let’s see an example to understand how a one-sided limit is calculated.
$$ \text{Evaluate} \lim\limits_{x \to 3} \frac{x^2-9}{x-3} $$ $$\lim\limits_{x \to 3} \frac{x^2-9}{x-3} $$ $$ \lim\limits_{x \to 3} \frac{(x+3)(x-3)}{x-3} = \lim\limits_{x \to 3}(x+3) $$ $$ \lim\limits_{x \to 3} (x+3) \;=\;3\;+\;3\;=\;6 $$
In this example, we only calculated the positive side limit of the given function.


