Sohcahtoa Calculator

The SOHCAHTOA calculator utilizes specific mnemonics to determine trigonometric values in right triangles. This helps you to solve the side lengths and angles of a right triangle along with the trigonometric functions of a right-angle triangle.

What Is SOHCAHTOA?

SOHCAHTOA is the term that enables you to remember the ratios of three main trigonometric functions: sine, cosine, and tangent.

It is the combination of three functions SOH, CAH, and TOA.

How to Calculate Trig Ratios Using SOHCAHTOA?

The mnemonic sohcahtoa is used to remember which function is used in what circumstances and is also used to find the trigonometric ratios of an acute angle of a triangle. 

• SOH = Perpendicular / Hypotenuse
• CAH = Base / Hypotenuse
• TOA = Perpendicular / Base 

Let us look at the sides of the triangle below and clarify this with the help of a diagram.

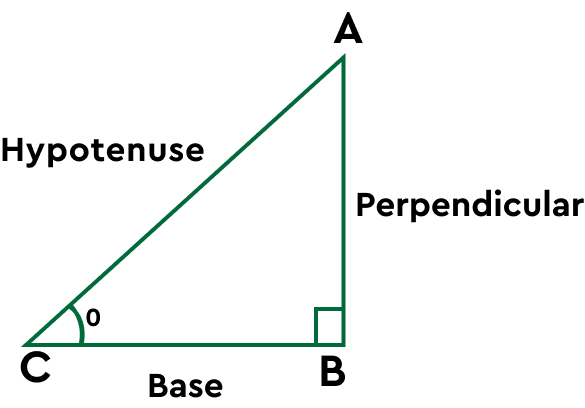
Perpendicular (Opposite)

It is the side that is opposite to the acute angle (θ). The side of a right triangle makes an angle of 90 degrees with the base. 

Base (Adjacent)

The adjacent side is the shorter side adjacent to the acute angle. The side on which the right triangle stands. It is connected to the acute angle and opposite. 

Hypotenuse (Diagonal)

The side that is always the opposite of the right angle is known as the hypotenuse. It is the longest side of the right triangle that is opposite to the 90-degree. 

SOHCAHTOA Table for Common Angles:

Trigonometric functions took some basic angle measurements. Therefore, some popular measurements of sohcahtoa measurements are as follows:

	$$ {\displaystyle \sin \theta } $$	$$ {\displaystyle \cos \theta } $$	$$ {\displaystyle \tan \theta =\sin \theta {\Big /}\cos \theta } $$
0° = 0 radians	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {blue}{0}} }}{2}}=\;\;0} $$	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {red}{4}} }}{2}}=\;\;1} $$	$$ {\displaystyle \;\;0\;\;{\Big /}\;\;1\;\;=\;\;0} $$
30° = π/6 radians	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {teal}{1}} }}{2}}=\;\,{\frac {1}{2}}} $$	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {orange}{3}} }}{2}}} $$	$$ {\displaystyle \;\,{\frac {1}{2}}\;{\Big /}{\frac {\sqrt {3}}{2}}={\frac {1}{\sqrt {3}}}} $$
45° = π/4 radians	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {green}{2}} }}{2}}={\frac {1}{\sqrt {2}}}} $$	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {green}{2}} }}{2}}={\frac {1}{\sqrt {2}}}} $$	$$ {\displaystyle {\frac {1}{\sqrt {2}}}{\Big /}{\frac {1}{\sqrt {2}}}=\;\;1} $$
60° = π/3 radians	$${\displaystyle {\frac {\sqrt {\mathbf {\color {orange}{3}} }}{2}}} $$	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {teal}{1}} }}{2}}=\;{\frac {1}{2}}} $$	$$ {\displaystyle {\frac {\sqrt {3}}{2}}{\Big /}\;{\frac {1}{2}}\;\,={\sqrt {3}}} $$
90° = π/2 radians	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {red}{4}} }}{2}}=\;\,1} $$	$$ {\displaystyle {\frac {\sqrt {\mathbf {\color {blue}{0}} }}{2}}=\;\,0} $$	$$ {\displaystyle \;\;1\;\;{\Big /}\;\;0\;\;=} Undefined $$

Measurements of SOHCAHTOA Ratios:

In calculus and analytic geometry, these ratios have a wide range of uses. So which are these and how these are calculated? Read on!

Basic Ratios

1. Sine: 

Sine = Perpendicular / Hypotenuse 

2. Cosine: 

Cosine = Base / Hypotenuse

3. Tangent: 

Tangent = Perpendicular / Base

4. Secant: 

Secant = Hypotenuse / Perpendicular

5. Cosecant: 

Cosecant = Hypotenuse / Base

6. Cotangent: 

Cotangent = Base / Perpendicular

Inverse Ratios

1. Arcsine:

Arcsine = sin^{-1}x

2. Arccosine:

Arccosine = cos^{-1}x

3. Arctangent: 

Arctangent = tan^{-1}x

4. Arcsecant:

Arcsecant = sec^{-1}x

5. Arccosecant:

Arccosecant = cosec^{-1}x

6. Arcotangent: 

Arcotangent = cot^{-1}x

Practical Example:

Suppose a right-angle triangle whose perpendicular (a) is equal to the 4cm and Angle β is 10 degrees. Calculate stepwise the other ratios.

Solution:

So for the final results use the sohcahtoa to find sides b, c, and after that angle and area. 
 
Find b;

$$ b=\sqrt{(c^2-a^2)} $$

$$ b=\sqrt{(4.061706447543^2-4^2)} $$

$$ b=\sqrt{(16.497459266012-16)} $$

$$ b=0.70530792283386 $$

Find c; 

$$ c=\sqrt{(a^2+b^2)} $$

$$ c=\sqrt{(4^2+0.70530792283386^2)} $$

$$ c=\sqrt{(16+0.49745926601221)} $$

$$ c=4.061706447543 $$

Certainly, you must demand how to find angles using sohcahtoa calculator. Look further calculations:

Find Angle α;

$$ \alpha= arctan(\dfrac{a}{b}) $$

$$ \alpha= arctan(\dfrac{4}{0.70530792283386}) $$

$$ \alpha= arctan(5.6712818196177) $$

$$ α=1.3962634015955 $$

Find Area;

$$ area=\dfrac{a*b}{2} $$

$$ area=\dfrac{4*0.70530792283386}{2} $$

$$ area= 1.4106158456677 $$ 

Steps To Use This Calculator:

Solve the trigonometric functions of a right-angle triangle with this sohcahtoa calculator by just inserting the below values in the calculator!

Input:

• Put two out of six values in the tool 
• Tap “Calculate”

Output:

• Sides of trigonometric ratios
• Find Angle α
• Area 
• Step-by-step calculations

FAQ:

What Is The Other Mnemonics for Remembering Triangle Trig Ratios?

Another collective phrase commonly used to recall the trig functions is seen below:

“Oscar Had A Heap Of Apples”

This implies that:

• Sin(θ) = Oscar / Had
• Cos(θ) = A / Heap
• Tan(θ) = Of / Apples

Is Sohcahtoa The Same As The Pythagorean Theorem?

In order to find the missing side of the right angle triangle we use the Pythagorean theorem and in order to memorize the trigonometric functions easily we use the sohcahtoa. 

References:

From the source Wikipedia: Mnemonics in trigonometry, sohcahtoa how to find angle, Hexagon chart.