What is Volume of Sphere? Its Formula, Derivation and way of Calculation
In this article, you will learn about the volume of a sphere formula. You will also learn how to calculate the volume of a sphere.
What is the Volume of a Sphere?
The volume of a sphere refers to the total space the sphere can occupy. In other words, it calculates the capacity of a sphere and how much space it can occupy. It is measured in m3, cm3, and inch3. A sphere is a three-dimensional shape, and the volume of the sphere is the measure of its capacity to occupy the space.
In mathematics, the volume of a sphere is an essential term because it enables you to find how much space is available in a package.
The Volume of a Sphere Formula
The formula of the volume of a sphere depends on the radius of the sphere which is given by:

Where r is the radius of the sphere. It means that the volume of a sphere is equal to the product of four by three of the pi and cube of the radius.
Volume of Sphere Formula Derivation
Consider the volume of a sphere made up of infinite thin circular disks. Consider one of these disks having radius r and thickness dy. The distance of this disk from the origin is y as shown in figure.
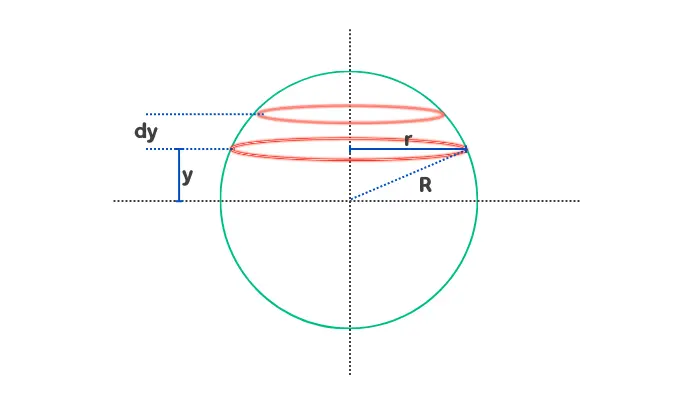

The volume of this disk element is dV which can be written as the product of the area of the disk and its thickness. So,
dV = (πr2)dy
Now,
dV = π(R2-y2)dy
Now to calculate the total volume of the sphere, we will use the integration method.
$$ \int dV \;=\; \int_{-R}^{+R} \; π(R^2-y^2)dy $$
$$ V \;=\; π(R^2y \;-\; \frac{1}{3}y^3)R -R $$
$$ V = π \Biggr[ R^2(R) \;-\; \frac{1}{3} R^3-R^2(-R) + \frac{1}{3} (-R^3) \Biggr] $$
By simplifying the above equation, we will get
$$ V \;=\; \frac{4}{3} πR^3 $$
Sphere Volume Formula with Diameter
Since the diameter is the full length of the line passing through a point on the sphere. And
$$ r \;=\; \frac{d}{2} $$Using this in the Formula of Volume.
$$ V \;=\; \frac{4}{3} π {\frac{d}{2}}^{3} $$Then the formula of sphere volume with diameter is:
$$ V \;=\; \frac{1}{6} πd^3 $$How to calculate the volume of a sphere?
You can calculate the volume of a sphere by using the formula: $$ V \;=\; \frac{4}{3} πR^3 $$
Where r is the radius of the sphere. Let’s see the following example to understand how the volume of the sphere is calculated.


Formulas Related to Volume of Sphere
There are some other formulas related to the volume of a sphere. These are:
- Cone Volume Formula
- Area of a Sphere Formula
- Pythagorean Theorem Formula
Cone Volume Formula
Generally, cone is a pyramid with a circular cross-section. So there is no difficulty to find the volume of a cone. The formula to find the cone volume is:
$$ V \;=\; \frac{1}{3} π r^2 h $$Area of a Sphere Formula
A sphere is a 3d and round shaped object that has no edges. The area covered by outer surface of the sphere is called the surface area of the sphere. The formula for sphere area is as follow:
$$ A \;=\; 4π r^2 $$Pythagorean Theorem Formula
The pythagorean theorem is a well knwown geometric formula that helps to calculate the length of bundary lines or sides of ny right angle triangle. The formula of pythagoras theorem is stated as:
$$ c^2 \;=\; a^2+b^2 $$FAQ’s
What is a Formula for the Volume of a Sphere?
The formula of the volume of a sphere is:
$$ V \;=\; \frac{4}{3} πR^3 $$How do you Find the Volume and Area of a Sphere?
The area of a sphere can be calculated by multiplying the square of radius with pi and 4. The formula is:
$$ A \;=\; 4πr^2 $$Similarly, the volume of the sphere can be calculated by using volume formula that is:
$$ V \;=\; \frac{4}{3} πR^3 $$Does a Circle have a Volume?
No, the circle does not have a volume because it is a two-dimensional shape. Two-dimensional shapes do not have any volume.


