What is Pythagorean Theorem Formula ? How to Use right Triangle Formula?
In this article, you will learn the Pythagorean Theorem and how it is used to solve the right triangle.
What is Pythagorean Theorem?
Pythagorean Theorem states that:
“In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of perpendicular and base.”
The Pythagorean Theorem is one of the most important mathematical concepts that explain the relation between the sides of a right triangle. It also helps to find the unknown side of a right-angled triangle. Using the Pythagorean Theorem, we can find the hypotenuse, base, and perpendicular of a triangle.
Pythagorean Theorem Formula:
If c is the hypotenuse and b is the base and a is the perpendicular, the Pythagorean Theorem formula can be written as:
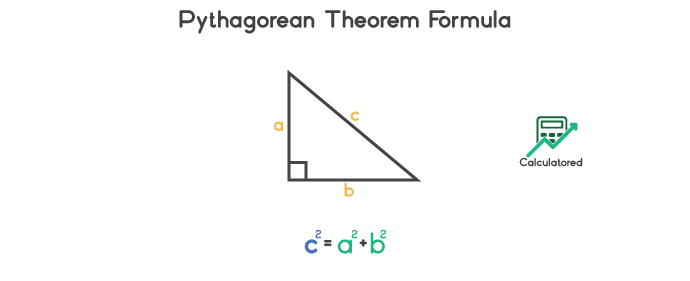

Here, c = Hypotenuse of triangle
a = Side of a triangle
b = Side of a triangle
If the hypotenuse is unknown, we can use the following hypotenuse formula derived from the Pythagorean formula,
$$ c \;=\; \sqrt (a^2 + b^2) $$
Pythagorean Theorem Proof
Given that:
“In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of perpendicular and base.”
To prove,
c2 = a2 + b2
Drawing a triangle ABC, and dividing it by an arc BD.
So we know from the figure that
$$ \triangle ADB \; \sim \; \triangle ABC $$
Therefore,
$$ \frac{AD}{AB} \;=\; \frac {AB}{AC} $$
Or,
$$ AB^2 \;=\; AD × AC……..(1) $$
Also,
$$ \triangle BDC \; \sim \; \triangle ABC $$ $$ \frac{CD}{BC} \;=\; \frac{BC}{AC} $$
Or,
$$ BC^2 \;=\; CD × AC……..(2) $$
By adding equation 1 and 2 we get,
$$ AB^2 + BC^2 \;=\; AB × AC + CD × AC $$ $$ AB^2 + BC^2 \;=\; AC(AD+CD) $$
Since AD+CD=AC,
$$ AB^2 + BC^2 = AC(AC) $$
So,
$$ AB^2 + BC^2 = AC^2 $$
Hence, the Pythagorean Theorem is proved.
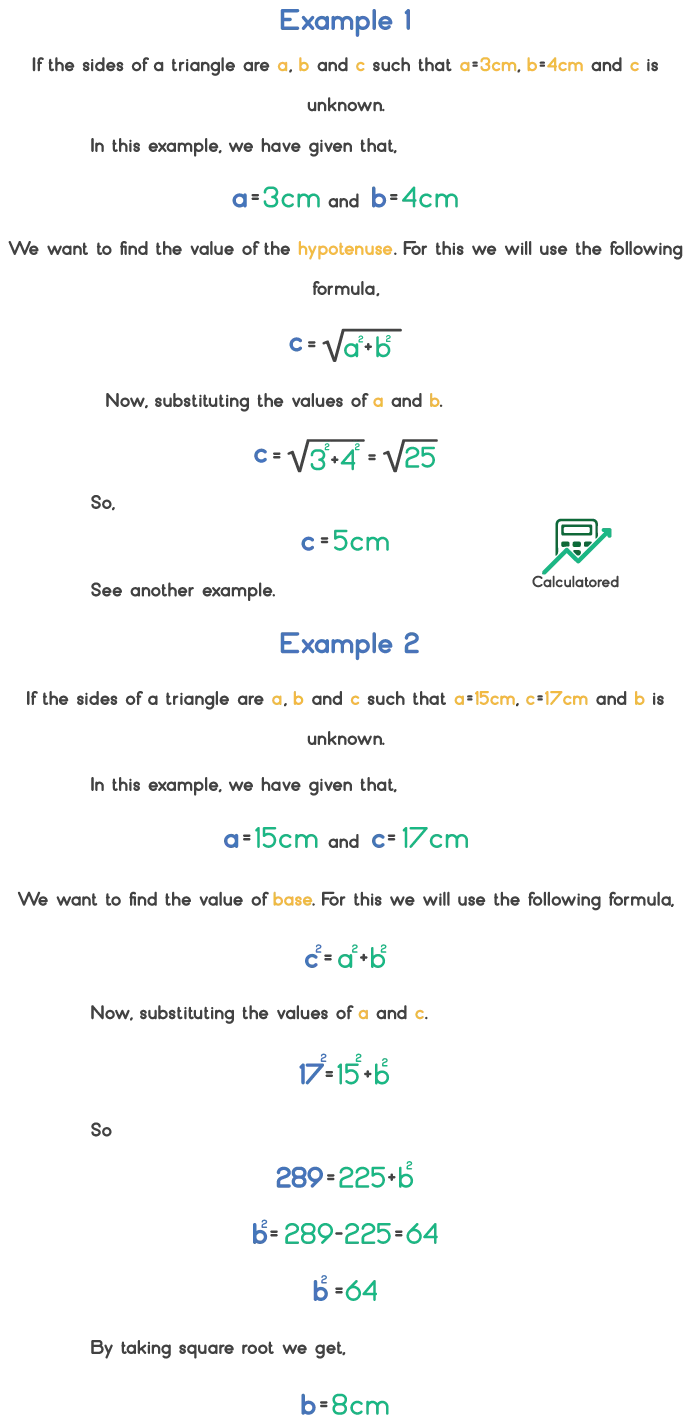
How to use the Pythagorean Formula?
The Pythagorean formula is also known as the right triangle formula. We can use it to find any unknown side of a triangle. See the below Pythagorean theorem examples to understand how it is helpful to calculate an unknown side of a triangle.

FAQ’s
How is the Pythagorean Theorem Related to the Distance Formula?
The Pythagorean Theorem is related to the distance formula because the distance formula is derived from Pythagorean Theorem. It helps to find the distance between two points in two dimensions. Basically, distance formula is the form of Pythagorean Theorem in 2D.
Where Pythagorean Theorem is Used?
It is used to find the length of sides of a right triangle. It is also used to find the length of the diagonal of a square.
What is Pythagorean Theorem?
Pythagorean Theorem states that:
“In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of perpendicular and base.”


