Kalkulator Titik Tengah

Pengantar Kalkulator Titik Tengah

Titik tengah adalah nilai tengah angka atau apa pun. Ini seperti memotong pizza berukuran delapan inci yang titik tengahnya adalah 4. Perhitungan titik tengahnya sama seperti kita menghitung rata-rata dua angka dengan menjumlahkan dan membaginya dengan dua. Kalkulator titik tengah adalah alat online untuk menghitung titik tengah segmen garis dengan koordinat.

Titik Tengah Segmen Garis

Pada gambar di bawah ini terdapat titik tengah ruas garis yang menghubungkan dua titik dengan mencari titik tersebut. Titik tengah kalkulator segmen garis dibuat sedemikian rupa sehingga dapat menemukan titik akhir dari titik tengah dan titik akhir dengan mudah. Jika Anda ingin menemukan nilai rata-rata yang tepat, coba Kalkulator Rata-rata.

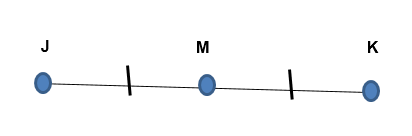
Titik tersebut berada tepat di tengah ruas garis sehingga memotongnya menjadi dua bagian yang kongruen. Dalam hal ini, Anda memiliki ruas garis JK dan titik M berada tepat di tengah. Jadi, JM adalah ½ dan KM adalah separuh lainnya. Keduanya kongruen.

$$JM\;=\;KM$$

Kalkulator ini mendukung untuk menghitung titik tengah dua titik A dan B pada suatu ruas garis. Sebenarnya kalkulator rumus titik tengah menggunakan koordinat dua titik seperti halnya

$$A(x^A,y^A)A(x^A,y^A)$$

sebaik

$$B(x^B,y^B)B(x^B,y^B)$$

"X" secara horizontal dan "Y" secara paralel

Formula Titik Tengah yang digunakan dalam Kalkulator Titik Tengah

Sekarang, kita akan mencari titik akhir dari titik tengah dan titik akhir pada bidang koordinat. Jadi kami ingin menganggap titik tengah sebagai lokasi dengan koordinat XY (x, y) dan kalkulator titik akhir kami untuk menemukan titik akhir dari titik tengah dan titik akhir menggunakan "rumus titik tengah"

$$(xm, ym) =({x^1+x^2\over 2},{y^1+y^2\over 2})\;$$

(x_m, y_m) berarti koordinat titik tengah

(x₁, y₁) Berarti koordinat titik pertama

(x_2, y₂) Berarti koordinat titik kedua

Kalkulator ini berurusan dengan menemukan titik tengah. Itu tidak akan menemukan jarak, karena jarak tidak diperlukan untuk pekerjaannya. Jika Anda perlu mencari rumus jarak, coba Kalkulator Rumus Jarak untuk menemukan nilai yang tepat.

Jadi, mari kita lanjutkan dan pelajari cara menggunakannya.

Contoh 1

Dalam contoh ini kita akan mengetahui tentang bagaimana mencari titik tengah.

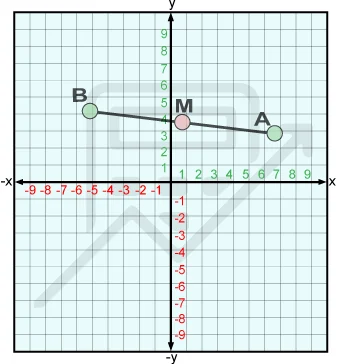
AB memiliki titik akhir di (7, 3) dan (-5,5). Plot titik M titik tengah AB.

Dalam contoh ini, kita ingin mencari titik tengah AB dan itu memberi kita koordinat (x, y) dari kedua titik ujung. Jadi mari kita mulai dengan memplot titik-titik akhir A pada 7, 3 dan B pada -5, 5 dan kemudian membangun ruas garis akan menjadi AB.

Jadi, kami ingin mencari titik tengah dari ruas garis ini secara manual tanpa menggunakan kalkulator titik tengah. Sekali lagi kita ingin mencari koordinat x, y, yang berada tepat di tengah ruas garis ini. Sehingga memotongnya menjadi dua bagian yang kongruen.

Di sini Koordinat A adalah (7,3) dan B (-5,5) jadi, sekarang gantilah nilai yang benar ke dalam rumus titik tengah. Sekarang titik akhir A dan B hanyalah koordinat XY.

Karena, (7,3) (-5,5) di sini di titik pertama 7 adalah x1 dan 3 adalah y1 sedangkan di titik kedua -5 adalah x2 dan 5 adalah y2.

$$=({x^1+x^2\over 2},{y^1+y^2\over 2})$$

Dengan meletakkan nilai dalam rumus titik tengah

$$=({7+(-5)\over 2},{3+5\over 2})$$ $$=({2\over 2},{8\over 2})$$ $$=(1,4)$$

Jadi dengan menggunakan titik-titik akhir tersebut dalam rumus titik tengah kita telah menemukan koordinat titik tengah AB pada 1, 4

Jadi kalkulator rumus titik tengah bekerja dengan benar dengan cara yang sama.

Apa itu Kalkulator Titik Tengah Kalkulator?

Kalkulator adalah portal web online yang menawarkan banyak kalkulator online dan konverter gratis. Kalkulator rumus titik tengah adalah salah satu alat yang dapat Anda gunakan tanpa biaya atau langganan apa pun. Kalkulator segmen garis kami akan langsung menghitung titik tengah X dan titik tengah Y dari koordinat yang berbeda secara online. Anda dapat menggunakan kalkulator titik akhir ini untuk menghemat waktu dan menyelesaikan tugas atau tugas Anda dengan cepat.

Bagaimana cara menggunakan Kalkulator Titik Tengah?

Kalkulator ini sederhana dan mudah digunakan. Anda akan menemukan kalkulator titik tengah sangat berguna untuk menemukan titik tengah. Cukup isi nilai ke dalam 4 kolom input untuk mendapatkan jawaban dengan cepat.

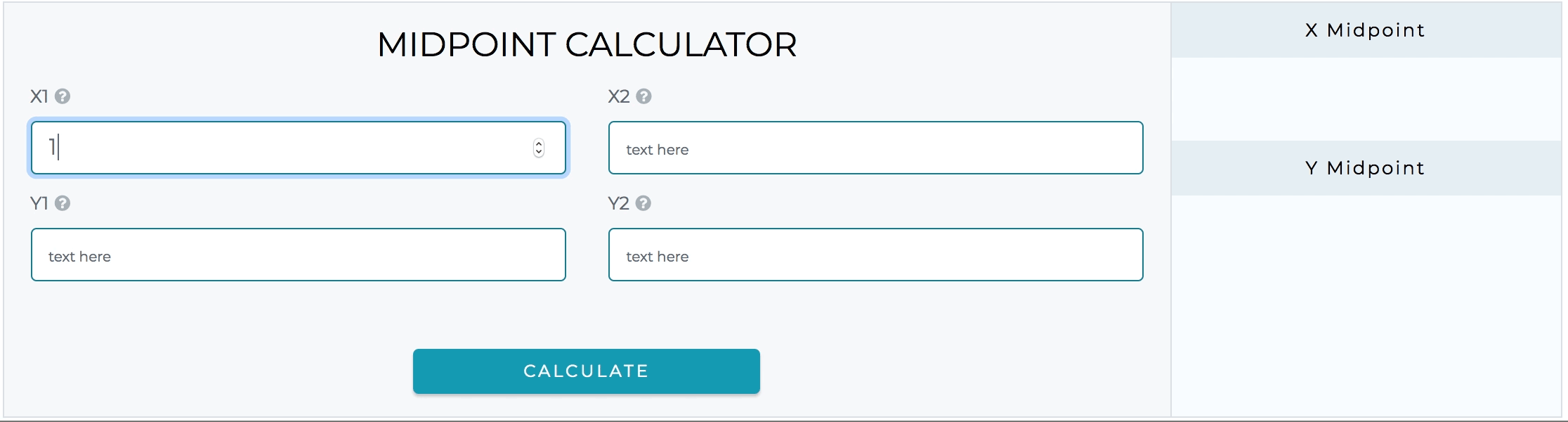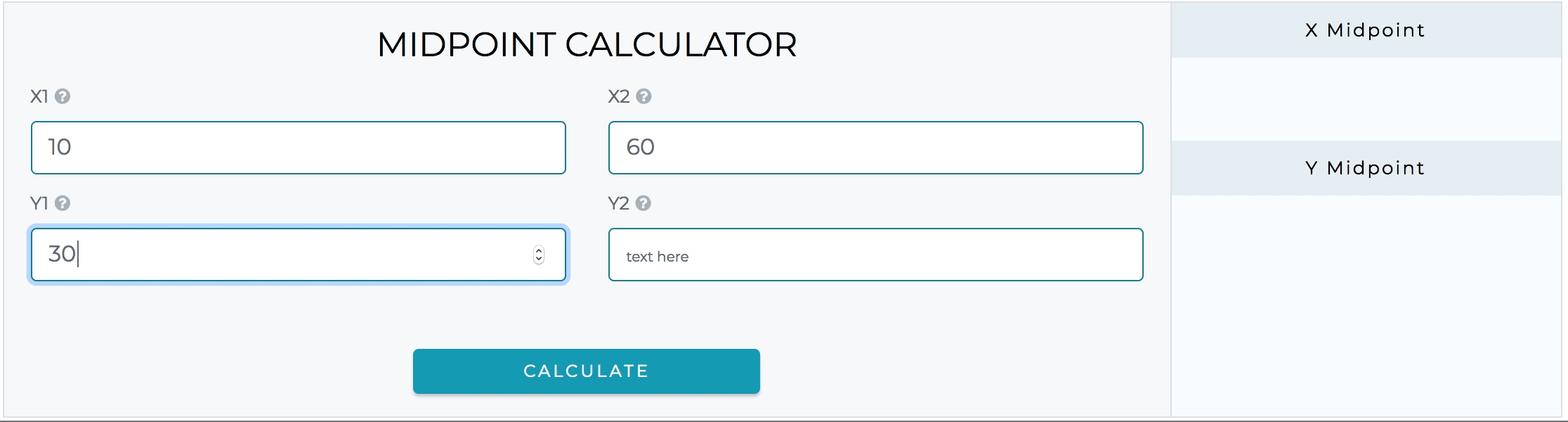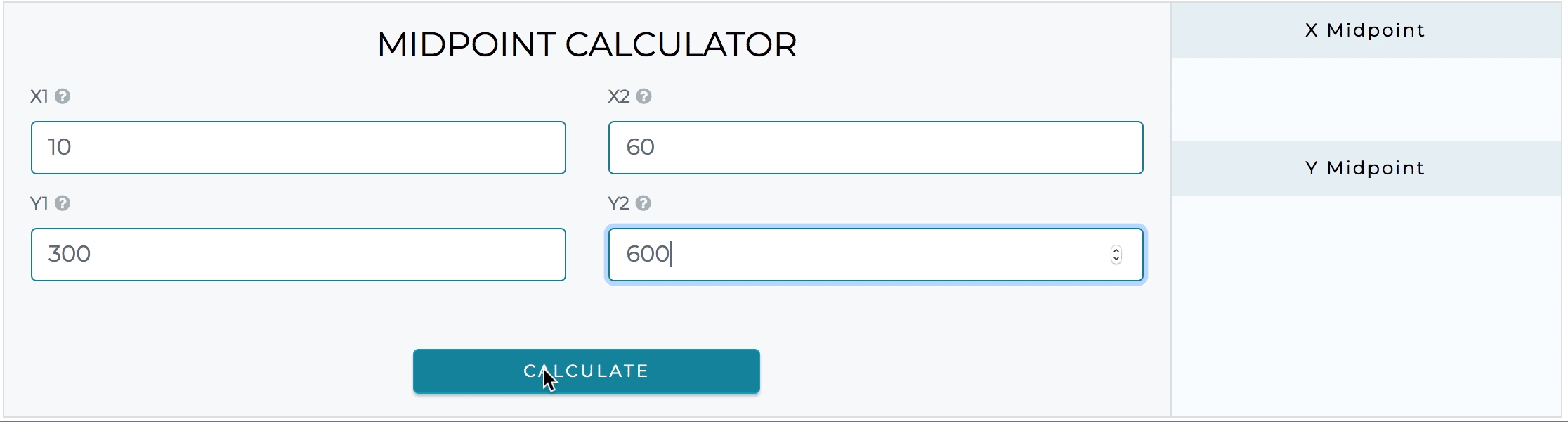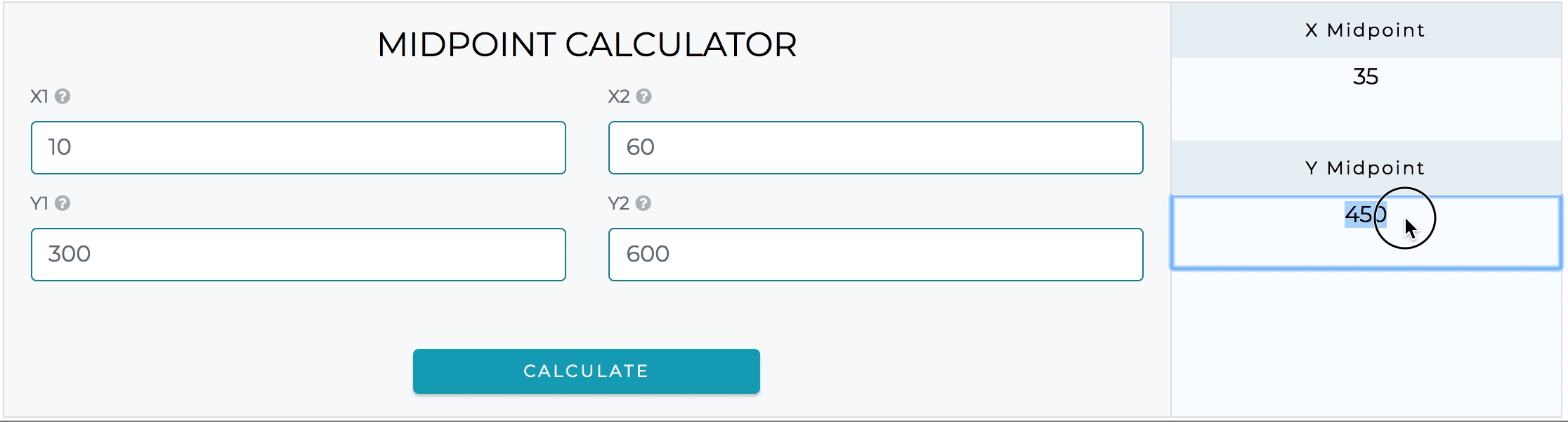
Kalkulator rumus titik tengah juga menyediakan bantuan untuk menyelesaikan jenis soal lanjutan ini. Jika ada yang ingin mencari titik akhir dari titik tengah, kalkulator titik akhir adalah alat online terbaik yang tersedia untuk tujuan ini.

Kalkulator aturan titik tengah mempraktikkan titik tengah setiap interval sebagai titik di mana memperkirakan fungsi untuk jumlah Rieman. Dalam jumlah Riemann aktual, nilai fungsi dan tinggi setiap persegi panjang sama di titik ujung kanan sedangkan di titik tengah jumlah Riemann, tinggi persegi panjang sama dengan nilai fungsi di titik tengahnya.