Área de uma esfera
Uma esfera é a forma de uma bola de basquete, é como um círculo tridimensional. Um pouco como um círculo, a escala de uma esfera é decidida por seu raio, que é a distância do meio da esfera a qualquer ponto em sua superfície. Pode ser descrito como o conjunto de todos os pontos situados a partir da distância r (raio) localizada em um determinado ponto (centro). é absolutamente simétrico e não possui arestas ou vértices.
A fórmula para encontrar a área da superfície de uma esfera é dada abaixo:
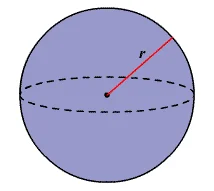
$$\text{Área}\;=\;4πr^2$$
Onde,
A figura acima pode visualizar como o volume de uma calculadora de esferas usa uma fórmula para calcular a área e o volume.
Essa fórmula foi descoberta pelo filósofo grego Arquimedes há mais de dois mil anos. Ele também percebeu que a área da superfície da esfera é exatamente igual à área da parede do seu circuito circuncrito de cilindro, que é o menor cilindro que pode conter uma esfera. Consulte Área de superfície de um cilindro.
Uma esfera tem várias características interessantes, uma delas é, uma esfera tem o maior volume, seguida, todas as outras formas com a mesma área de superfície.
Reorganizando uma fórmula dada acima, você pode encontrar o raio:
$$r\;=\;\sqrt{\frac{a}{4π}}$$
onde "a" é uma área da superfície de uma esfera.
Volume de uma esfera
Uma esfera é um conjunto de pontos no espaço que estão localizados em uma distância distante do centro.
O volume é um espaço ocupado por qualquer sólido tridimensional. O volume é medido em unidades cúbicas, como in³, ft³, cm³, m³ etc.
O volume V de uma esfera é 4/3 vezes de raio ao cubo e pi.
$$\frac {4}{3} πr^3$$
O volume de um hemisfério é 1/2 do volume da esfera relacionada.
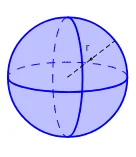
Volume de uma esfera
$$=\;\frac {4}{3} πr^3$$
Onde r é o raio da esfera. Na figura acima, a calculadora Volume de uma esfera é usada para encontrar o volume da esfera e também se concentrar em como eles o calculam. Como 4, 3 e pi são valores constantes, isso simplifica para aproximadamente
$$4.19r^3$$
Reorganizando a fórmula dada acima, você pode encontrar o raio:
$$r\;=\;\sqrt[3]{\frac{3v}{4π}}$$
onde v é o volume de uma esfera.
Circunferência de uma esfera
A circunferência de um círculo ou esfera é igual a 6,2832 vezes mais do raio. A circunferência de um círculo ou esfera é igual a 3,1416 vezes mais que o diâmetro.
A fórmula para encontrar a circunferência de uma esfera é mencionada abaixo:
$$C\;=\;2πr$$
Diâmetro de uma esfera
O diâmetro de um círculo ou esfera é igual a 2 vezes mais que o raio. A fórmula para calcular o diâmetro da esfera é:
$$D\;=\;2r$$
Coisas para recordar
Calculadora de volume de uma esfera
Calculado introduza a calculadora Volume de uma esfera para usar no cálculo do volume de uma esfera.

Onde,
Primeiro você tem que inserir o valor do raio, então há uma aba no botão onde você deve inserir a unidade do raio. Você verá três opções:
Depois de inserir o raio referente à sua unidade, pressione o botão “CALCULATE” e a calculadora Volume de uma esfera calculará o volume e a circunferência da esfera.
Aqui está o exemplo de cálculo para encontrar a área e o volume da esfera por meio da calculadora Volume de uma esfera calculada pela Calculadora.

Depois de inserir o raio referente à sua unidade, pressione o botão “CALCULATE” e a calculadora de Volume de uma esfera calculará o volume e a circunferência da esfera nos blocos à direita.
- r é o raio da área da superfície da esfera.
- π o valor de pi é 3.14 ou 3.14159. É a razão entre a circunferência de qualquer círculo e o diâmetro do círculo.
- Área de superfície da esfera = 4πr2
- Volume de uma esfera = 4/3 πr3
- Você só precisa conhecer o raio para calcular o volume e a área de uma esfera.
- As respostas dos problemas da área de superfície devem sempre estar em unidades quadradas
- As respostas aos problemas de volume devem sempre estar em unidades cúbicas
- Raio em centímetros
- Raio em metros
- Raio em milímetros

