Volume Kalkulator Sphere

Luas Sebuah Bola

Bola adalah bentuk bola basket, itu seperti lingkaran tiga dimensi. Sedikit seperti lingkaran, skala bola ditentukan oleh jari-jarinya, yaitu jarak dari tengah bola ke titik mana pun di permukaannya. Ini dapat digambarkan sebagai himpunan semua titik yang terletak dari jarak r (radius) yang terletak pada titik tertentu (pusat). itu benar-benar simetris, dan tidak memiliki tepi atau simpul.

Rumus untuk mencari luas permukaan bola diberikan di bawah ini:

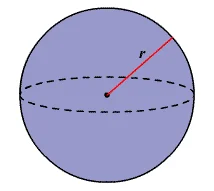
$$\text{Area}\;=\;4πr^2$$

Dimana,

• r adalah jari-jari luas permukaan bola.
• π nilai pi adalah 3,14 atau 3,14159. Ini adalah rasio keliling lingkaran apa pun dengan diameter lingkaran.

Gambar di atas akan memvisualisasikan bagaimana volume kalkulator bola menggunakan rumus untuk menghitung luas dan volume.

Formula ini ditemukan oleh filsuf Yunani Archimedes lebih dari dua ribu tahun yang lalu. Ia juga menyadari bahwa luas permukaan sebuah bola sama persis dengan luas dinding lengkung silinder yang dibatasi, yaitu silinder terkecil yang dapat menampung bola tersebut. Lihat Luas permukaan silinder.

Sebuah bola memiliki beberapa sifat yang menarik, salah satunya adalah bola memiliki volume terbesar dari semua bentuk lainnya dengan luas permukaan yang sama.

Dengan menyusun ulang rumus yang diberikan di atas, Anda dapat menemukan jari-jari:

$$r\;=\;\sqrt{\frac{a}{4π}}$$

dengan "a" adalah luas permukaan bola.

Volume Sphere

Bola adalah sekumpulan titik dalam ruang yang terletak pada jarak r tertentu dari pusat.

Volume adalah jumlah ruang yang ditempati oleh benda padat 3 dimensi. Volume diukur dalam satuan kubik seperti in³, ft³, cm³, m³ dll. Pastikan semua pengukuran harus dalam satuan yang sama sebelum menghitung volume.

Volume V bola adalah 4/3 kali jari-jari kubik dan pi.

$$\frac {4}{3} πr^3$$

Volume sebuah belahan adalah 1/2 volume dari bola yang terkait.

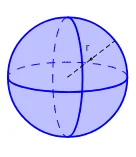
Volume Sphere

$$=\;\frac {4}{3} πr^3$$

Dimana r adalah jari-jari bola. Pada gambar di atas, kalkulator Volume bola digunakan untuk mencari volume bola dan juga fokus pada cara mereka menghitungnya. Karena 4, 3 dan pi adalah nilai konstan, ini disederhanakan menjadi kira-kira

$$4.19r^3$$

Dengan menyusun ulang rumus yang diberikan di atas, Anda dapat menemukan jari-jari:

$$r\;=\;\sqrt[3]{\frac{3v}{4π}}$$

dengan v adalah volume bola.

Lingkar bola

Keliling lingkaran atau bola sama dengan 6,2832 kali lebih besar dari Radius. Keliling suatu lingkaran atau bola sama dengan 3,1416 kali lebih besar dari Diameternya.

Rumus untuk mencari keliling bola disebutkan di bawah ini:

$$C\;=\;2πr$$

Diameter bola

Diameter lingkaran atau bola sama dengan 2 kali lebih besar dari Radius. Rumus untuk menghitung diameter bola adalah:

$$D\;=\;2r$$

Hal-hal yang perlu diingat

• Luas permukaan bola = 4πr²
• Volume bola = 4/3 πr³
• Anda hanya perlu mengetahui jari-jari untuk menghitung volume dan luas bola.
• Jawaban soal luas permukaan harus selalu dalam satuan persegi
• Jawaban soal volume harus selalu dalam satuan kubik

Volume kalkulator bola

Kalkulator memperkenalkan Volume kalkulator bola yang akan digunakan untuk menghitung volume bola.

Dimana,

Pertama Anda harus memasukkan nilai radius, lalu ada tombol tab down dimana Anda harus memasukkan satuan radius. Anda akan melihat tiga opsi:

• Radius dalam sentimeter
• Radius dalam meter
• Radius dalam milimeter

Setelah Anda memasukkan radius sesuai dengan satuannya kemudian tekan tombol “HITUNG” dan kalkulator Volume bola akan menghitung volume dan keliling bola.

Berikut adalah contoh penghitungan untuk mencari luas dan volume bola melalui kalkulator Volume bola yang dihitung.

Setelah memasukkan radius sesuai satuannya kemudian tekan tombol “HITUNG” dan kalkulator Volume bola akan menghitung volume dan keliling bola pada balok sebelah kanan.