Definición de desviación estándar
¿Qué es la desviación estándar? La definición de desviación estándar es una cantidad específica que expresa qué cantidad de miembros de un grupo dado son diferentes del valor medio para el grupo.
KarI Pearson presentó por primera vez el concepto de desviación estándar en la última década del siglo XVIII. En realidad, es una medida de variación entre valores dados en un grupo. La DE siempre se calcula a partir de la media aritmética, no de la mediana o la moda. Se denota con el símbolo de sigma (σ)
Fórmula de desviación estándar
La fórmula de desviación estándar para la población es:
$$SD\;=\;σ\;=\;\sqrt\frac{\sum(x-µ)^2}{n}$$
En esta fórmula ∑ significa la suma del valor de la variable de observación, mientras que x es cada valor en el conjunto de datos dado y µ es la media del conjunto de datos dado de la población yn significa el número total de elementos.
Si está tratando con cualquier conjunto de datos de muestra, la fórmula de desviación estándar de la muestra será:
$$SD\;=\;σ\;=\;\sqrt\frac{\sum(x-x)^-2}{n-1}$$
¿Cómo calcular la desviación estándar?
Método de cálculo de la desviación estándar paso a paso.
- Encuentre la media (Μ) de los datos dados.
- Reste la media (Μ) de cada valor dado. El resultado se denominará la desviación de la media.
- Tome el cuadrado de cada desviación de la media.
- Descubra la suma de los cuadrados tomados
- Luego, divida su total por el número (N) que se llamará varianza.
- Luego, tome la raíz cuadrada de la varianza. El resultado se denominará desviación estándar.
La calculadora de desviación estándar funciona de la misma manera que se indicó anteriormente.
Ejemplo de desviación estándar
Aquí hay un ejemplo que aclarará cómo calcular la desviación estándar.
Ejemplo 1:
Los puntajes de las pruebas de matemáticas de diferentes estudiantes son: 91, 91,91,41,51
Para calcular la desviación estándar de la clase dada, seguiremos los pasos dados anteriormente.
$$\sqrt\frac{\sum(18+18+18-32-22)^2}{n}$$
$$\sqrt\frac{324+324+324+1024+484}{5}$$
$$\sqrt\frac{2480}{5}$$
$$SD\;=\;σ\;=\;\sqrt496$$
$$SD\;=\;σ\;=\;22.27105745132$$
Ahora veámoslo de acuerdo con los pasos dados anteriormente.
-
Encuentra la media Μ
(91 + 91 + 91 + 41 + 51) / 5 = 73
-
Calcular la desviación de la media
91 – 73 = 18, 91 – 73 = 18, 91 – 73 = 18, 41 – 73 = -32, 51 – 73 = -22
-
Cuadrada de cada desviación de la media
(18)2 = 324, (18)2 = 324, (18)2 = 324, (-32)2 = 1,024, (-22)2 = 484
-
Calcular la suma de todos los cuadrados
324 + 324 + 324 + 1,024 + 484 = 2,480
-
Divida el total de los cuadrados tomados por el número de elementos (N)
2,480 / 5 = 496
-
Hallar la raíz cuadrada de la varianza
$$\sqrt496=22$$
La desviación estándar también ayuda a aprender los conceptos de cuadrática y trapezoide. Para los cálculos, puede utilizar nuestra calculadora de fórmula cuadrática y calculadora de área trapezoidal.
Ejemplo 2:
Diferentes clases de física tomaron la misma prueba con cinco calificaciones>
90, 90, 90, 50, 50
Calcule la desviación estándar de la clase.
p>$$SD\;=\;σ\;=\;\sqrt\frac{\sum(x-µ)^2}{n}$$
$$SD\;=\;σ\;=\;\frac{\sum(x-µ)^2}{n}$$
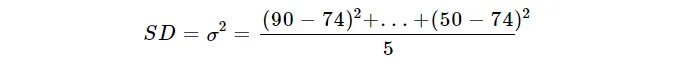
$$=\frac{1920}{5}$$
$$=384$$
$$=\sqrt384$$
$$=19.595917942265$$
error estándar
En estadística, una media muestral difiere de la media real del conjunto de datos de población dado; esta desviación se llama error estándar de la media. El error estándar ocurre cuando llevamos a cabo una investigación y, en su mayoría, recopilamos solo pequeños datos de muestra de esa población específica solo porque encontramos una ligera diferencia entre el conjunto de valores cada vez. Por otro lado, si tomamos suficientes muestras de la población, la media se organizará automáticamente en la distribución de la media real de la población.
Existe una ligera diferencia entre la desviación estándar y el error estándar, es decir, una DE indica la cantidad de variabilidad y dispersión de la media para un conjunto de datos dado, pero la SE de la media indica la divergencia entre la media muestral de datos y la media real de la población. El error estándar de la media siempre será menor que la desviación estándar.
La fórmula para calcular el error estándar es:
$$SE\;=\;\frac{σ}{\sqrt(n)}$$
El error estándar es útil para precisar la media de los datos dados de esa población específica que probablemente se compararía con la media de la población real.
Unidades de desviación estándar
¿La desviación estándar tiene unidades como otros valores estadísticos? La respuesta es que la desviación estándar se expresa en las mismas unidades que los datos originales.
Cálculo de la desviación estándar entre dos conjuntos de datos
La desviación estándar cuantifica cómo se diferencian los valores de su conjunto de datos y es útil para determinar qué tan diferentes son sus números entre sí.
Los datos son 3, 7, 7, 19 frente a 2, 5, 6, 7
- Recopile sus datos para crear el conjunto de datos a partir del cual desea calcular la desviación estándar.
- Calcule el promedio o la media del conjunto de datos sumando todos los números del conjunto y dividiendo el total por el número de elementos de su conjunto.
(3 + 7 + 7 + 19) / 4 = 9
vs
(2 + 5 + 6 + 7) / 4 = 5
Aquí la media es 5
-
Reste la media del primer número de su conjunto de datos y eleve al cuadrado las diferencias
3 – 9 = -62 = 36, 7 – 9 = -22 = 4, 7 – 9 = -22 = 4, 19 – 9 = 102 = 100
Vs
2 – 5 = -32 = 9, 5 – 5 = 02 = 0, 6 – 5 = 12 = 1 7 – 5 = 22 = 4
-
Sume las diferencias al cuadrado y luego divida el total por el número de elementos en Data Se
36 + 4 + 4 +100 = 144
144 / 4 = 36
Vs
9 + 1 + 4 = 14
-
Tome la raíz cuadrada de esta media de diferencias para encontrar la desviación estándar.
$$\sqrt36=6$$
Vs
$$\sqrt14=3.74$$


