Puede usar la calculadora de longitud de arco para calcular la longitud de arco de un círculo o también puede encontrar la longitud de arco manualmente. Un círculo es siempre igual a 360° y se compone de puntos consecutivos alineados en 360 grados. Si divides el grado del arco medido por 360°, descubrirás la fracción de la circunferencia del círculo que forma el arco.
$$\text{arc length}\;= s\;=\;r\;\theta$$
Esta es la forma manual de encontrar la longitud del arco. También puede encontrar la calculadora longitud de arco en términos de pi para encontrar con precisión la longitud del arco.
Fórmula de grados de la calculadora de longitud de arco
La calculadora de fórmulas de longitud de arco utiliza la siguiente fórmula:
$$\text{Arc length}\;=\;2πR\;*\;\frac{C}{360}$$
dónde:
C = ángulo central del arco (grados)
R = es el radio del círculo
π = es Pi, que es aproximadamente 3,142
360 ° = ángulo completo
Recuerde que la circunferencia de todo el círculo es 2πR, por lo que la Fórmula de longitud del arco anterior simplemente reduce esto dividiendo el ángulo del arco a un ángulo completo (360).
Con la implementación de la fórmula de longitud de arco anterior, la calculadora de longitud de arco resuelve fácilmente el ángulo central, el radio o la longitud del arco.
¿Qué es la fórmula de longitud de arco (radianes)?
Si el ángulo central es radianes, entonces la fórmula de la longitud del arco es más simple:
$$\text{arc length}\;= \;R\;*\;C$$
dónde:
C = es el ángulo central del arco (radianes)
R = es el radio del arco
La fórmula de longitud de arco (radianes) es la misma que el método utilizado en la versión de grados, pero en los grados, el 2π / 360 convierte los grados a radianes. El cálculo de radianes y la calculadora de longitud de arco le permite encontrar resultados haciendo simples clics.
Otra forma de medir ángulos en lugar de grados son los radianes. Un radianes equivale aproximadamente a 57,3 °. Para la dispersión o variación de un conjunto de valores, pruebe la Calculadora de división estándar.
¿Qué es el área del círculo?
Podemos definir el área del círculo de las siguientes formas:
- Todo el espacio dentro de la circunferencia de un círculo se llama área de ese círculo.
- El número total de unidades cuadradas dentro de un círculo se llama área de ese círculo.
- El área del espacio dentro del círculo se llama área de ese círculo.
¿Cómo encontrar el área de un círculo?
La calculadora de longitud de arco es la mejor manera de encontrar el área de un círculo. La fórmula básica para encontrar el área de un círculo es:
$$A = π r^2$$
Dónde:
A = Área del círculo
r = Radio del círculo
π = Constante matemática cuyo valor es 22/7 o 3,14.
¿Cómo calcular el área de un círculo?
En la clase de geometría, un problema común es calcular el área del círculo dependiendo de la información dada. Sin embargo, la fórmula (A = π r2) es simple y solo necesitamos saber el radio del círculo para encontrar su área. También necesitamos practicar la conversión de algunos otros bits de los datos dados en términos que puedan ayudarnos a usar esta fórmula.
Hay dos formas principales a través de las cuales podemos calcular el área de un círculo. La forma tradicional y la forma digital. Con la forma digital, necesitará una calculadora longitud de arco. Algunas terminologías importantes para calcular el área de un círculo se describen a continuación:
Calcular el área de un sector de un círculo
- Circunferencia (C):
La circunferencia de un círculo es el límite circundante de ese círculo.
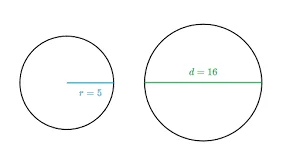
- Radio (r):
La longitud de una línea desde cualquier punto del límite del círculo hasta el centro del círculo se conoce como radio del círculo.
- Diámetro (d):
El diámetro es la longitud de la línea que atraviesa el círculo a través del centro del círculo.
- Pi (π):
Pi es una constante matemática cuyo valor es aproximadamente 3,14
Ahora discutimos los métodos,
- Método 1:
Pi es una constante matemática cuyo valor es aproximadamente 3,14
Calcular el área a partir del diámetro
Si conocemos el diámetro de un círculo, el área se puede encontrar usando la siguiente fórmula:
$$Area = πD^2/4$$Donde D es el diámetro y Pi = 3,14
- Método # 2:
Calcular el área a partir de la circunferencia
Si conocemos la circunferencia de un círculo, entonces el área se puede encontrar como:
$$Area= C^2 /4π$$Donde C es la circunferencia del círculo.
- Método # 3:
- Sector:
Un sector se define dibujando dos radios desde el centro hasta el borde del círculo. El espacio entre estos dos radios se llama sector.
Si conocemos el área de un sector y la medida de su ángulo central, entonces:
Acir = Asec * 360 / C
Dónde,
Acir = Área del círculo.
Asec = Área del sector.
C = medida del ángulo central.
¿Cómo encontrar la longitud de la curva?
La longitud de una curva o línea es la longitud de la curva. La longitud de un arco se puede encontrar siguiendo la fórmula para cualquier curva diferenciable.
Estas curvas se definen mediante ecuaciones rectangulares, polares o paramétricas. Vea el arco de un círculo para conocer la longitud de un arco circular.
Calculadora de longitud de arco para fórmula de curva:
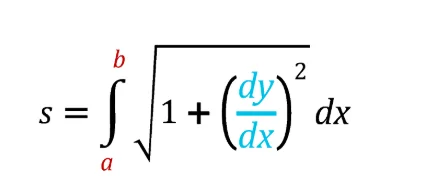
donde a y b representan los valores x, y, t o θ, según corresponda, y DX es el pequeño cambio en X e Y que también se puede encontrar. Calculadora de longitud de arco con la misma fórmula para obtener resultados precisos.
$$\text{arc length}\;= s\;=\;r\;\theta$$
Para conocer el límite de una función, ecuación y fórmula, busque nuestra "Calculadora de límites" de forma gratuita.
¿Cómo encontrar la calculadora de fórmulas de longitud de arco?
La calculadora de radios y longitud de arco con pi se puede encontrar fácilmente en línea. Existen numerosas calculadoras de medida de arco, pero necesita encontrar la mejor. La herramienta que muestra el ángulo central, el radio y el diámetro será la mejor calculadora longitud de arco.
¿Cómo usar la calculadora de longitud de arco?
Calculatored introduce la calculadora longitud de arco en términos de pi para el cálculo de la longitud de arco:
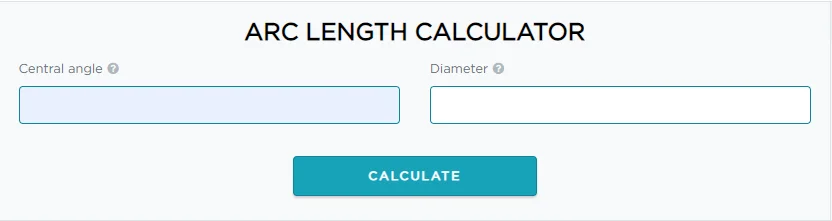
Simplemente siga los pasos a continuación para calcular la longitud del arco paso a paso.
Paso # 1: Ingrese el valor del ángulo central.
Paso # 2: Ingrese el valor de Radio.
Paso # 3: Ingrese el valor de Diámetro.
Paso # 4: Haga clic en el botón "CALCULAR".
Aquí está el ejemplo para calcular la longitud del arco a través de la calculadora de fórmula de longitud de arco.
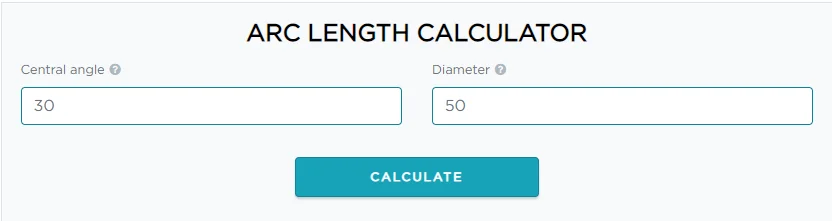
Después de hacer clic en el botón calcular, la calculadora de radianes y longitud de arco le mostrará instantáneamente los resultados precisos en términos de ángulo central, radio y diámetro junto con la longitud del arco.

