Calcul Ecart Type

Qu'est-ce que l'écart type?

L'écart type est un terme qui mesure la quantité de variation ou de dispersion d'un ensemble de valeurs. Si les valeurs sont proches de la moyenne de l'ensemble, ce sera un faible écart type. Si les valeurs sont réparties dans une plage plus large, ce sera un écart type élevé.

Le concept d'écart type a été présenté par KarI Pearson au 18e siècle. L'écart type est la mesure de la variation entre des valeurs données dans un groupe. SD est toujours calculé à partir de la moyenne arithmétique et non à partir de la médiane ou du mode. Il est désigné par le symbole de sigma (σ)

Formule d'écart type

La formule d'écart-type pour la population est :

$$SD=σ=\sqrt\frac{\sum(x-µ)^2}{n}$$

Dans la formule d'écart type, ∑ signifie la valeur de sommation de l'observation. x est la valeur dans l'ensemble de données donné et µ est la moyenne de l'ensemble de données donné de la population et n signifie le nombre total d'éléments.

Pour chaque ensemble de données, l'échantillon de formule d'écart type sera :

$$SD=σ=\sqrt\frac{\sum(x-x)^-2}{n-1}$$

Comment calculer l'écart type?

Suivez les étapes ci-dessous pour calculer l'écart type étape par étape :

Étape 1 : Découvrez la moyenne (µ) des données données.

Étape #2 : Soustraire la moyenne (µ) de chaque valeur donnée (écart par rapport à la moyenne).

Étape 3 : faites le carré de chaque écart de la moyenne.

Étape 4: Découvrez la somme des carrés pris.

Étape #5 : Divisez son total par le nombre (n) qui sera appelé variance.

Étape #6 : Prenez la racine carrée de la variance, le résultat sera appelé l'écart type.

Comment trouver l'écart type?

Afin d'apprendre à trouver l'écart type, résolvons un exemple.

Les résultats des tests de mathématiques des différents élèves sont : 91, 91, 91, 41, 51.

Pour trouver l'écart type de la classe donnée, nous utiliserons la formule d'écart type.

$$SD= σ =\sqrt\frac{\sum(x-µ)^2}{n}$$

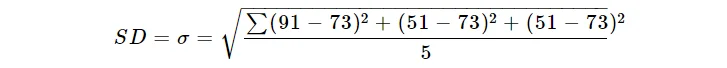
$$\sqrt\frac{\sum(18+18+18-32-22)^2}{n}$$

$$\sqrt\frac{324+324+324+1024+484}{5}$$

$$\sqrt\frac{2480}{5}$$

$$SD= σ =\sqrt496$$

$$SD= σ =22.27105745132$$

 

Les étapes ci-dessous nous aideront à trouver l'écart type

Étape 1 : Trouvez la moyenne M

(91 + 91 + 91 + 41 + 51) / 5 =

Étape #2 : Calculer l'écart par rapport à la moyenne

91 – 73 = 18, 91 – 73 = 18, 91 – 73 = 18, 41 – 73 = -32, 51 – 73 = -22

Étape 3 : carré de chaque écart par rapport à la moyenne

(18)² = 324, (18)² = 324, (18)² = 324, (-32)² = 1 024, (-22)² = 484

Étape 4: Calculez la somme de tous les carrés

324 + 324 + 324 + 1 024 + 484 = 2 480

Étape #5 : Divisez le total des carrés pris par le nombre d'éléments (n)

2 480 / 5 = 496

Étape #6 : Trouvez la racine carrée de la variance

$$\sqrt496=22$$

Comment calculer l'écart type de la classe?

Disons qu'une classe de physique a passé un test avec des scores de 90, 90, 90, 50, 50 et nous devons calculer l'écart type pour la classe.

$$SD= σ =\sqrt\frac{\sum(x-µ)^2}{n}$$

$$SD= σ^2 =\frac{\sum(x-µ)^2}{n}$$

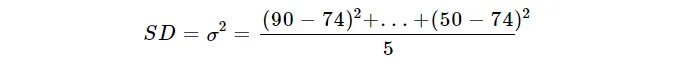
$$=\frac{1920}{5}$$

$$=384$$

$$=\sqrt384$$

$$=19.595917942265$$

Notre portail dispose également d'un calculateur de log et d'un calculateur antilog pour les étudiants et les enseignants. Vous pouvez découvrir gratuitement les formules, les équations et les calculs du logarithme et de l'antilogarithme sur notre site Web.

Qu'est-ce que l'erreur standard?

La moyenne de l'échantillon diffère de la moyenne réelle de l'ensemble de données de la population ; cet écart est appelé erreur standard de la moyenne. L'erreur standard se produit lorsque nous collectons de petits échantillons de données ou trop d'échantillons de population, la variation provoque une différence entre les ensembles de valeurs.

Déviation standard vs erreur standard

L'écart type diffère de l'erreur type. L'écart type indique la quantité de variabilité et de dispersion par rapport à la moyenne des données. L'erreur standard indique la divergence entre la moyenne de l'échantillon et la moyenne réelle de la population.

L'erreur type de la moyenne est toujours inférieure à l'écart type. Le calculateur d'erreur standard calcule l'équation d'écart type et trouve l'erreur standard (SE).

Formule d'erreur standard

La formule d'erreur standard pour calculer l'erreur standard est

$$SE=\frac{σ }{\sqrt(n)}$$

L'erreur standard est utile pour vous de préciser la moyenne des données données de cette population spécifique qui serait probablement comparée à la moyenne réelle de la population.

Ecart type entre deux ensembles de données

L'écart type trouve la différence dans les nombres et la diversité des valeurs de l'ensemble de données.

Si les données sont 3, 7, 7, 19 vs 2, 5, 6, 7. Suivez les étapes ci-dessous pour calculer SD entre deux ensembles de données. Les étapes sont

Étape 1 : Collectez des données pour créer un ensemble de données afin de calculer l'écart type.

Étape 2 : Calculez la moyenne et la moyenne de l'ensemble de données en additionnant tous les nombres et en divisant le total par le nombre d'éléments dans l'ensemble de données.

(3 + 7 + 7 + 19) / 4 = 9 contre (2 + 5 + 6 + 7) / 4 = 5

Ici la moyenne est de 5

Étape 3 : Soustrayez la moyenne du premier nombre de votre ensemble de données et placez les différences au carré.

3 – 9 = -6² = 36, 7 – 9 = -2² = 4, 7 – 9 = -2² = 4, 19 – 9 = 10² = 100

Vs

2 – 5 = -3² = 9, 5 – 5 = 0² = 0, 6 – 5 = 1² = 1 7 – 5 = 2² = 4

Étape n° 4 : Ajoutez des différences au carré et divisez le total par le nombre d'éléments dans l'ensemble de données.

36 + 4 + 4 +100 = 144

144 / 4 = 36

Vs

9 + 1 + 4 = 14

Étape n°5 : Prenez la racine carrée de cette moyenne des différences pour trouver l'écart type.

$$\sqrt36=6$$

Vs

$$\sqrt14=3.74$$

C'est ainsi que nous calculons l'écart type entre deux ensembles de données.

Qu'est-ce que le calculateur d'écart type?

Comme d'autres concepts mathématiques, trouver l'écart type peut être difficile si nous n'avons pas le concept approprié. Calculated a introduit un calculateur d'écart type en ligne qui prend l'entrée et fournit des résultats précis instantanément.

Comment utiliser le calculateur d'écart type?

Le calculateur d'écart type est rapide, précis et gratuit. Il vous suffit d'entrer les valeurs de l'ensemble de données et notre calculateur d'écart type gratuit calculera instantanément les valeurs de moyenne, d'écart type (SD) et de variance.