Calculateur de longueur d'arc

Vous pouvez trouver la longueur d'arc manuellement et en utilisant le calculateur de formule de longueur d'arc. Un cercle est toujours égal à 360° et il est constitué de points consécutifs alignés à 360 degrés. Si vous divisez le degré de l'arc mesuré par 360°, vous découvrirez la fraction de la circonférence du cercle que constitue l'arc.

Ensuite, si vous multipliez cette fraction par la circonférence du cercle, la longueur approche autour du cercle, vous obtiendrez la longueur de l'arc. La formule pour la longueur de l'arc est

$$\text{arc length}\;= s\;=\;r\;\theta$$

C'est la façon manuelle de trouver la longueur de l'arc. Vous pouvez également trouver un calculateur de longueur d'arc en termes de pi pour trouver avec précision la longueur de l'arc.

Formule de degré du calculateur de longueur d'arc

Le calculateur de formule de longueur d'arc utilise la formule ci-dessous:

$$\text{Arc length}\;=\;2πR\;*\;\frac{C}{360}$$

où:

C = angle au centre de l'arc (degré)

R = est le rayon du cercle

π = est Pi, qui est d'environ 3,142

360° = Plein angle

N'oubliez pas que la circonférence de tout le cercle est de 2πR, donc la formule de longueur d'arc ci-dessus réduit simplement cela en divisant l'angle de l'arc en un angle complet (360).

Qu'est-ce que la formule de longueur d'arc (radians)?

Si l'angle au centre est en radians, la formule de la longueur de l'arc est plus simple:

$$\text{arc length}\;= \;R\;*\;C$$

où:

C = est l'angle au centre de l'arc (radians)

R = est le rayon de l'arc

La formule de longueur d'arc (radians) est la même que la méthode utilisée dans la version degrés, mais dans les degrés, le 2π/360 convertit les degrés en radians. Le calcul du calculateur de radians et de longueur d'arc vous permet de trouver des résultats en faisant de simples clics.

Les radians sont une autre façon de mesurer les angles au lieu des degrés. Un radian équivaut approximativement à 57,3° . 

Qu'est-ce que l'aire de cercle?

Nous pouvons définir l'aire du cercle de la manière suivante:

• Tout l'espace à l'intérieur de la circonférence d'un cercle est appelé l'aire de ce cercle.
• Le nombre total d'unités carrées à l'intérieur d'un cercle est appelé aire de ce cercle.
• L'aire de l'espace à l'intérieur du cercle est appelée l'aire de ce cercle.

Comment trouver l'aire d'un cercle?

Le calculateur de longueur d'arc est le meilleur moyen de trouver l'aire d'un cercle. La formule de base pour trouver l'aire d'un cercle est:

$$A = π r^2$$

Où:

A = Aire du cercle
r = Rayon du cercle
π = Constante mathématique dont la valeur est 22/7 ou 3.14.

Comment calculer l'aire d'un cercle?

En classe de géométrie, un problème courant est de calculer l'aire du cercle en fonction des informations données. Même si, la formule (A = π r2) est simple et il suffit de connaître le rayon du cercle pour trouver son aire. Nous devons également nous entraîner à convertir d'autres bits des données données dans les termes qui peuvent nous aider à utiliser cette formule.

Il existe deux manières principales de calculer l'aire d'un cercle. La voie traditionnelle et la voie numérique. Avec la manière numérique, vous aurez besoin d'un calculateur de longueur d'arc. Certaines terminologies importantes du calcul de l'aire d'un cercle sont décrites ci-dessous:

• Circonférence (C):

  La circonférence d'un cercle est la limite englobante de ce cercle.

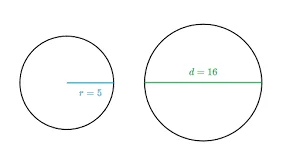
• Rayon (r) :

  La longueur d'une ligne de n'importe quel point de la limite du cercle au centre du cercle est appelée rayon du cercle.

• Diamètre (d) :

  Le diamètre est la longueur de la ligne qui traverse le cercle en passant par le centre du cercle.

• Pi (π):

  Pi est une constante mathématique dont la valeur est d'environ 3,14

  Maintenant, nous discutons des méthodes,

• Méthode n°1 :

  Pi est une constante mathématique dont la valeur est d'environ 3,14

  Calcul de l'aire à partir du diamètre

  Si nous connaissons le diamètre d'un cercle, l'aire peut être trouvée en utilisant la formule suivante :

  $$Area = πD^2/4$$

  Où D est le diamètre, et Pi = 3,14

• Méthode n°3 :

  Calcul de l'aire à partir d'un secteur de cercle

• Secteur:

  Un secteur est défini en traçant deux rayons du centre vers le bord du cercle. L'espace entre ces deux rayons est appelé secteur.

  Si l'on connaît l'aire d'un secteur et sa mesure d'angle au centre, alors :

  A_cir = A_sec * 360/C

  Où,

  A_cir = Aire du cercle.

  A_sec = Aire du secteur.

  C = mesure de l'angle au centre.

Comment trouver la longueur de courbe?

La longueur d'une courbe ou d'une ligne est la longueur de la courbe. La longueur d'un arc peut être trouvée en suivant la formule pour toute courbe différentiable.

Ces courbes sont définies par des équations rectangulaires, polaires ou paramétriques. Voir arc de cercle pour la longueur d'un arc de cercle.

Calculateur de longueur d'arc pour la formule de courbe :

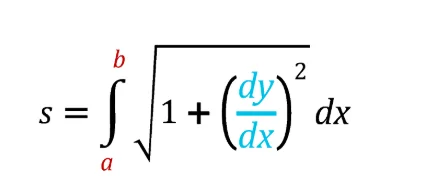
où a et b représentent les valeurs x, y, t ou selon le cas, et DX est le petit changement de X et Y peut également être trouvé. Longueur du calculateur d'arc la même formule pour des résultats précis.

$$\text{arc length}\;= s\;=\;r\;\theta$$

Pour apprendre la limite d'une fonction, d'une équation et d'une formule, trouvez gratuitement notre calculateur de limite.

Comment trouver le calculateur de formule de longueur d'arc?

Le calculateur de rayon en radians et de longueur d'arc avec pi peut être trouvé facilement en ligne. Il existe de nombreuses calculatrices de mesure d'arc, mais vous devez trouver la meilleure. L'outil qui vous montre l'angle central, le rayon et le diamètre sera la meilleure longueur de calculateur d'arc.

Comment utiliser le calculateur de longueur d'arc ?

Calculatored présente le calculateur de longueur d'arc en termes de pi pour le calcul de la longueur d'arc :

Suivez simplement les étapes ci-dessous pour calculer la longueur de l'arc étape par étape.

Étape 1 : Entrez la valeur de l'angle central.

Étape 2 : Entrez la valeur du rayon.

Étape #3 : Entrez la valeur du diamètre.

Étape 4: Cliquez sur le bouton "CALCULER".

Voici l'exemple pour calculer la longueur de l'arc via le calculateur de formule de longueur d'arc.

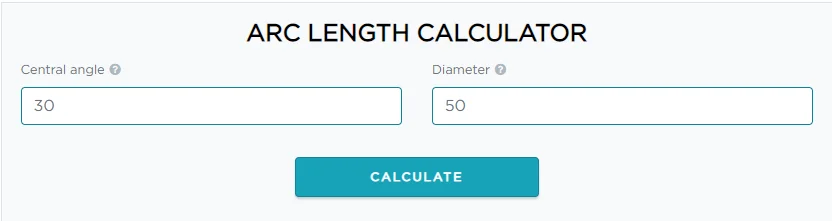
Après avoir cliqué sur le bouton calculer, le calculateur de radians et de longueur d'arc vous montrera instantanément les résultats précis en termes d'angle central, de rayon et de diamètre ainsi que la longueur de l'arc.