What is binary number system?
Binary number is a base-2 number system that concerns with only two digits 0s and 1s. Computer works according to binary numbers, meaning computer storing and processing data and calculating tasks by using 0s and 1s. Binary is the primary language for the computer. We generally deals with the decimal system in our daily life.
How to convert the binary to decimal?
Conversion process is very simple and easy:
- Note the leftmost number of your initial number. Multiply by 2.
- Add the next number of the binary number. The sum will be your new "initial number".
- Keep repeating these steps, each time first multiplying by 2 and then adding the last digit.
For example, for the binary number 111001, we would have the following steps:
$$1 * 2 = 2$$
$$(2 + 1) * 2 = 6$$
$$(6 + 1) * 2 = 14$$
$$(14 + 0) * 2 = 28$$
$$(28 + 0) * 2 $$
$$ = 56 56 + 1 = 57 $$
Binary to Decimal Table:
| Binary | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
How to convert the binary to hex?
binary to hex conversion process is very simple and easy:
- Take the binary numbers, starting from the right side of the binary number, divide into groups,each group consists of the 4 binary numbers.
- Convert each group of 4 binary digits to its equivalent hex value.
- Combine the results together, giving the total hex number.
Binary to HexaDecimal Table:
| Binary | HexaDecimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
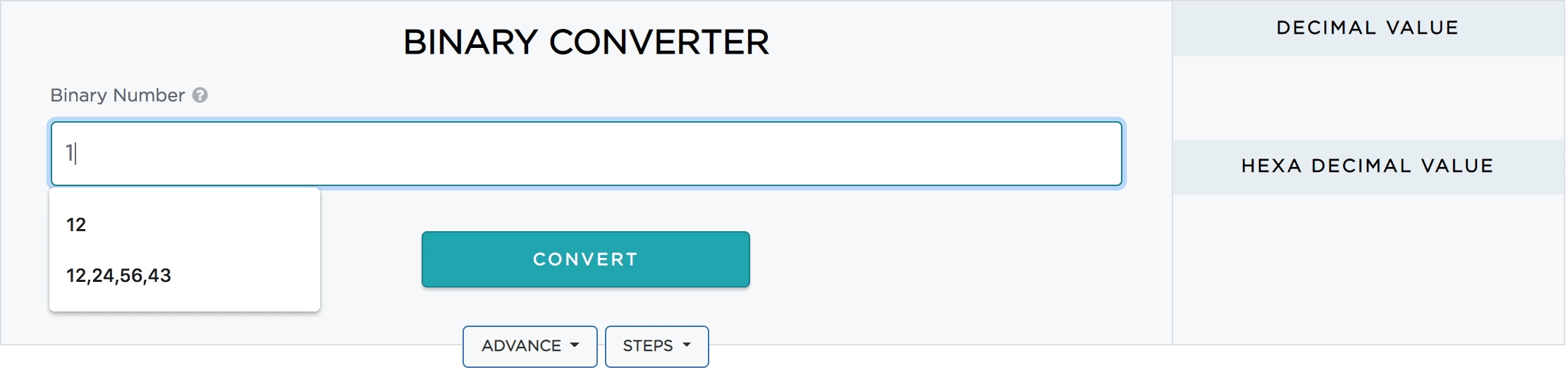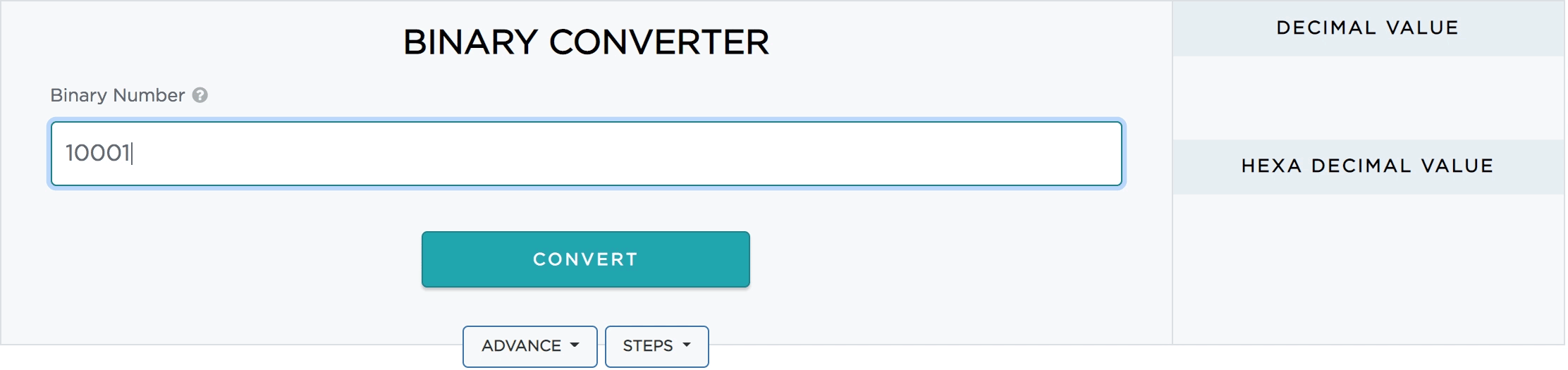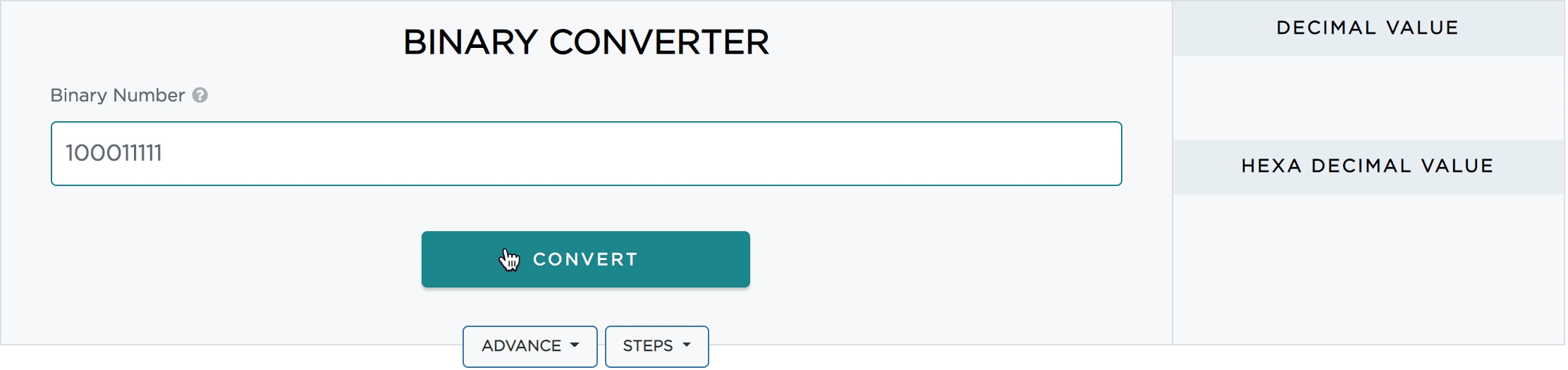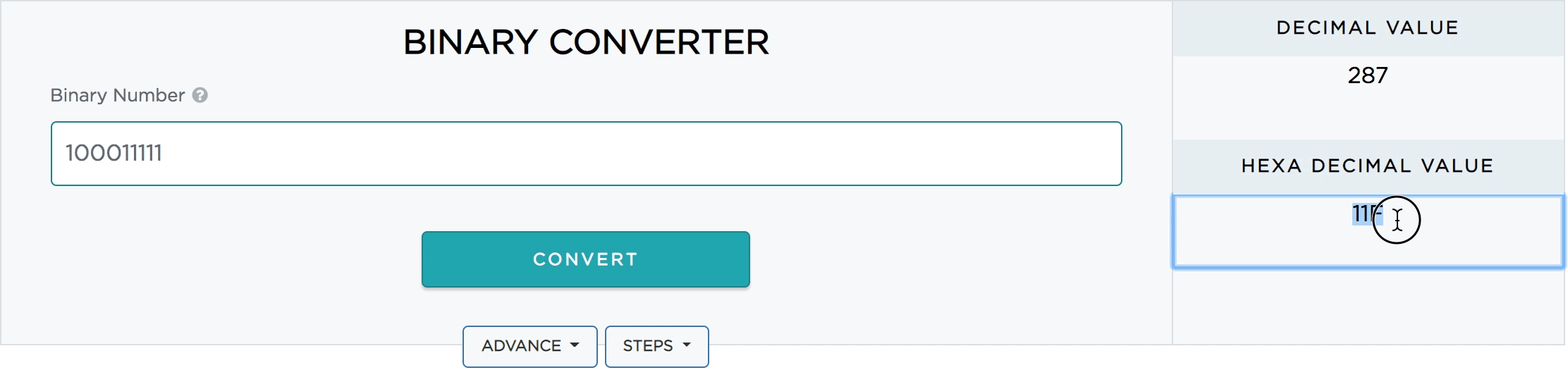
How To Use Binary Converter?