The decimal, also termed as the denary or base 10 numbering system is what we use in everyday life for calculating. We use these numbers in situations where we need accuracy.
Sometimes, we need number based conversions for various tasks; for instance, we need binary numbers to manipulate or transfer data in computer. On the other hand, if you want to solve math problems regarding fractions you have to change the base 10 number. We have the solution to your problems, we offer a free online converter to help you in the routine operations regarding number systems.
Our Decimal converter is designed to transform decimals to fractions, binary numbers, and hexadecimals. In this article you will learn the basics of these conversions.
Decimal to Fractions:
1) To make a fraction, write the decimal number as the top number (numerator) and 1 as the bottom number (denominator).
2) Now, count the number places to the right of the dot. Let’s consider 2 number places are at the right side, multiply 100 with both the numerator and denominator.
3) Simplify this fraction by finding the Greatest Common Factor (GCF) of both numerator and denominator and divide both by that number.
4) Last step is to reduce the remaining fraction, if possible.
Example
Convert 0.48 to fraction:
$$\frac{0.48}{1} = \frac{0.48*100}{1*100} = \frac{48}{100}$$
$$(48,100) GCF = 4$$
$$ = \frac{48}{4} * \frac{100}{4} = \frac{12}{25} $$
How to convert repeating decimals to fraction?
- Make an equation where x equals the number.
- By counting the numbers at right to decimal Y. Write another equation multiplying both sides of the first equation by the 10y
- Deduct the second equation from the first.
- Solve to get value for x
- Simplify the fraction.
Example: Convert the repeating fraction 4.666
x= 4.666…………….. (1), y= 3 (1000) multiply on both sides
1000x= 4666.666……………. (2)
By Subtracting (1) from (2) 999x = 4662
X= 4662/333/999/333 = 14/3
OR use our Decimal Converter instead to instantly compute the results.
How to convert Decimal to Binary?
The binary numbering system, is the foundation for data storage, transfer and handling of data in computer systems and digital electronic tools. This system has base 2 rather than 10 which we are acquainted with for routine calculations.
Now what to do for converting decimal to binary?
For the base 10 number system conversion to base 2 numbers you can use the remainder method. This includes dividing the number by 2 repeatedly until you have 0, while noting down each remainder.
- Note down the given number.
- Divide it by 2.
- Keep writing the result underneath, while writing the remainder on the right hand side, this will be 0 or 1.
- Continue to divide and write the remainders until you get the required result of 0.>
- The most significant bit (MSB) is at the lowermost of the remainder column and the least significant bit (LSB) is the uppermost number.
- The binary equivalent is read from bottom to top, from MSB to LSB.

Tired of repeated divisions? Or need something quicker? We have the right tool for you, our Decimal Converter will save your day with speedy conversion.
Decimal to Hex Conversion:
Hex has an advantage in digital hardware system as it allows us to use 4 times fewer bits that makes it more useful than binary. Moreover, no processor works with anything less than 4bits, so, it is the most suitable system to express numbers for digital hardware.
Wait! How would you convert the number to hex?
- First, divide the number by 16.
- Write the quotient and again divide that by 16.
- Keep on dividing till you get 0.
- Note the remainders on the right side and convert to hex.
| Division by 16 | Quotient | Remainder(dec) | Remainder(hex) | Digit # |
|---|---|---|---|---|
| 7562/16 | 473 | 10 | A | 0 |
| 472/16 | 29 | 8 | 8 | 1 |
| 29/16 | 1 | 13 | D | 2 |
| 1/16 | 0 | 1 | 1 | 3 |
$$7562 = 1D8A\;hex$$
You will have to go through all these basic steps to change the number systems, but if you use our decimal to hex converter, it will assist you to transform these numbers efficiently and quickly with zero margin of error.
We hope that you can benefit from this article, and solve problems regarding the number based conversions. Are you interested in some of our other tools? Have a look at our other recommended tools like Hex Converter and Binary converter.
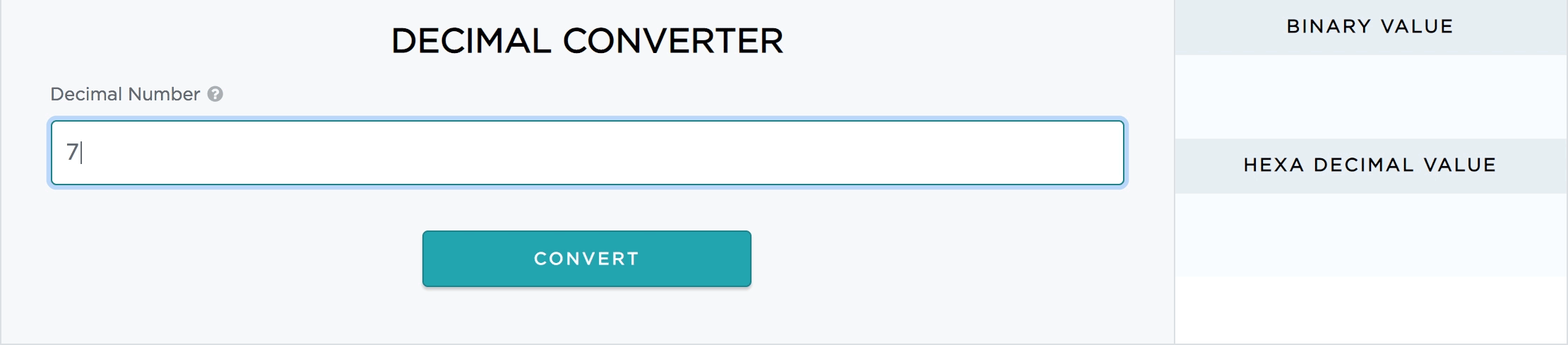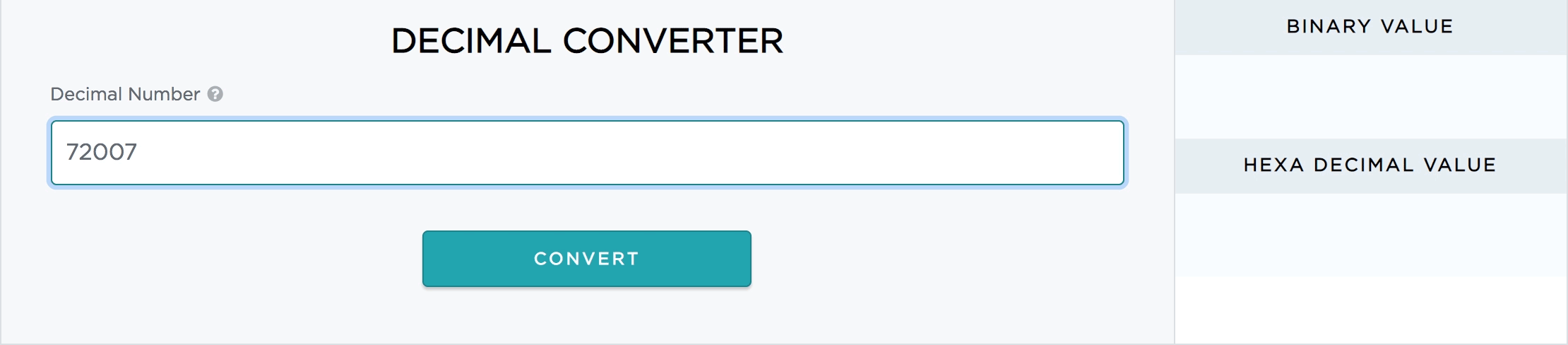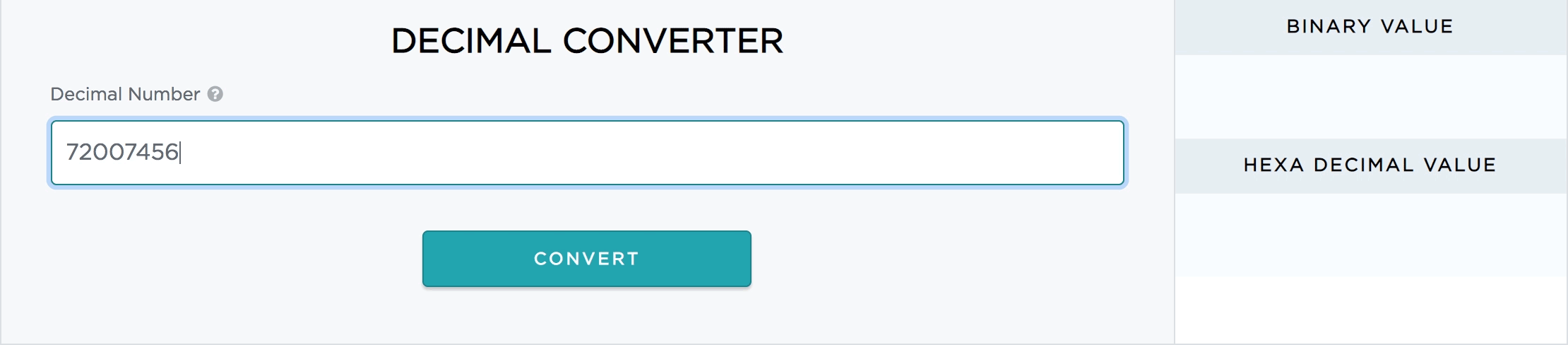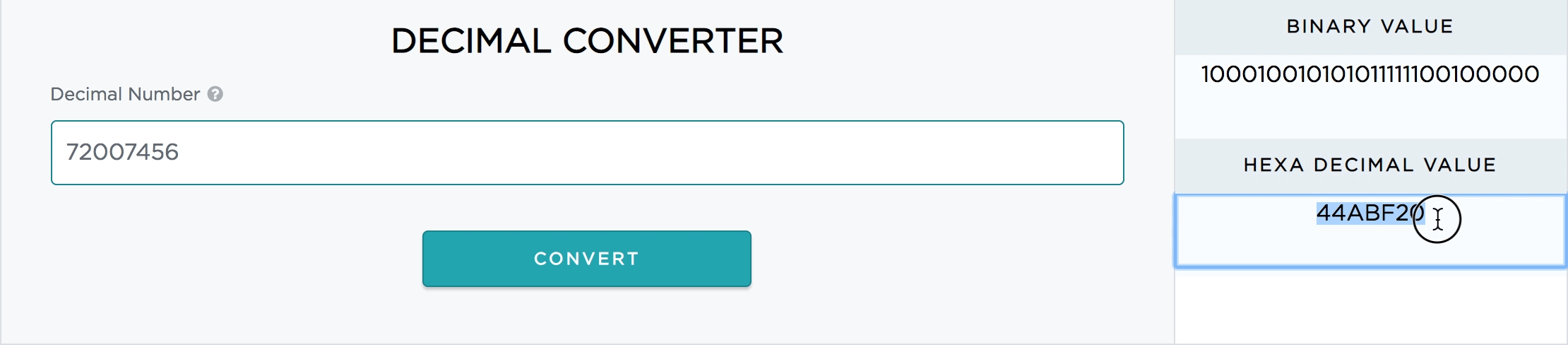
How To Use Decimal Converter?