What is Voltage Divider?
Voltage divider is a passive linear circuit whose output voltage is a fraction of its input voltage. Voltage divider is responsible for distributing input voltage in the components of the circuit.
What is Voltage Divider Circuit?
Consider a box that can contain a single source or any other combination of circuit elements. It will be hooked up to a few resistors that are all lined up in parallel and we need to calculate the voltage drop across each of the resistors.
As per the Kirchhoff’s Current Law and Kirchhoff’s Voltage Law (KVL), the cumulative drop in potential (voltage) across all of the series resistors will sum to the value coming out of our source (box). The voltage potential will start at the value of the source and drop a certain percentage as each of the resistors elements is encountered.
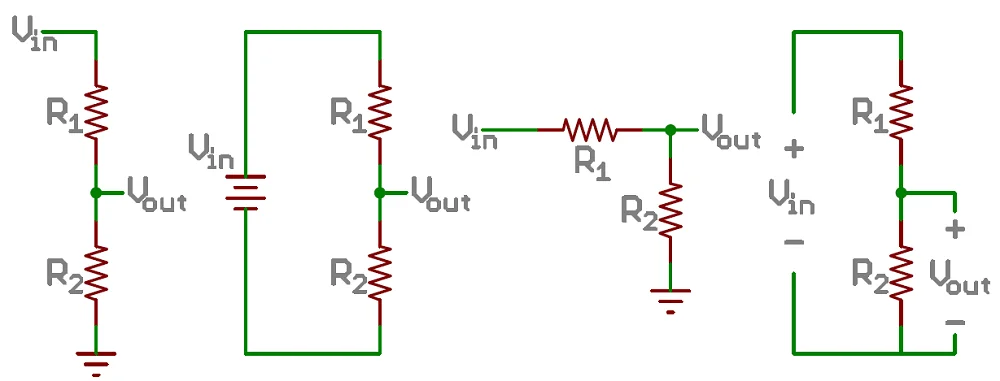
To calculate the voltage dropped across the 1st resistor, voltage source is multiplied by the value of that resistor and divided by the total resistance.
The resulting value is the voltage drop across the first resistor. Consequently, that leaves Vin - V resistor1 as the value left to drop across the second resistor.
How to calculate Voltage?
Consider the circuit which we mentioned above, using two resistors R1 and R2. Both the R1 and R2 resistors are in series so
Ohm's law
By ohm's law, we get V=IR
As we have two resistors, so the above equation becomes
V1 =R1i …………… (1)
V2 = R2i …………… (2)
Kirchhoff's Voltage law
Now applying Kirchhoff's voltage law
-V +v1 +v2 =0
V = V1 +v2
Therefore, the equation becomes
V (t) =R1i + R2i = (R1+R2)
Hence
i (t) =v /R1+R2……………. (3)
Substituting 3 in 1 and 2 equations, we get
V1 = R1 (v /R1+R2)
V (R1/R1+R2)
V2 = R2 (v /R1+R2)
V (R2/R1+R2)
Equation of Voltage Divider
We already drive the voltage divider rule equation, which uses three input values in any circuit, input voltage and two resistor’s values. By utilizing the accompanying condition, we can discover the yield voltage
Vout = Vin x R2/R1+R2
From the above condition, we infer the yield voltage is legitimately relative to the information voltage and the proportion of two resistors R1 and R2.
Learn more about the calculations of frequency & wavelength using frequency calculator and wavelength calculator online.
How to find Vout or Output Voltage?
Example 1: Let’s assume a circuit has two resistors R1 and R2 with the values of 1kΩ and 3kΩ respectively. The Vin or input voltage of the circuit is 12V.
As per voltage divider equation,
Vout = Vin R2 / R1 + R2
By putting the values of Input voltage and R1 and R2 in this equation, we get
Vout = 12V. 3kΩ/ 1kΩ + 3kΩ
Vout = 12V. 3kΩ/4kΩ
Vout = 12V 3 / 4= 9V
So the output voltage is 9V.
We can check output voltage & connect resistors to bring the output voltage down.
What is Voltage Divider Calculator?
Being human, we can make mistakes to lead unwanted results. To overcome this, Calculatored brings you the best solution for calculating voltage. A voltage divider calculator can find the right output voltage for complex circuits.
Our voltage divider calculator is free and easiest tool to use. It utilizes a pure voltage divider equation or formula to solve your numerical problems efficiently.
How to use Voltage Divider Calculator?
Voltage divider calculator is very simple & easy to use. Steps of using voltage divider calculator are
Step #1: Enter Voltage Source (For Input Voltage)
Step #2: Enter Resistance 1 (R1 in Ohm)
Step #3: Enter Resistance 2 (R2 in Ohm)
Step #4: Click on "CALCULATE" button.
Once you click on calculate button, You will get your output voltage within a few seconds, making our voltage divider calculator the easiest to use.

