Kalkulator Matriks

pengantar

Hari ini kita akan membahas cara kerja Kalkulator Matriks. Matriks matematika sebenarnya adalah kumpulan elemen, tersusun dalam baris dan kolom serta kombinasi persamaan linier. Dalam matematika matriks,

angka 1, 2, 3, 4, ..... n

disebut entri atau elemen matriks. Matriks diwakili oleh simbol berikut (), [], || ||, mis.

$$\left[\begin{matrix} 2 & 1 & 3 \\ 4 & 2 & 1 \\ 3 & 3 & 2 \\ \end{matrix}\right] 3*3 $$

Ada banyak jenis matriks misalnya; matriks baris, matriks kolom, matriks persegi, matriks nol, matriks identitas, matriks diagonal, matriks skalar, matriks segitiga, matriks transpos, matriks simetris, matriks skew, matriks setara, matriks aljabar. Sekarang kita akan mengetahui bagaimana kalkulator matriks menjalankan fungsinya. Tidak diragukan lagi, matriks memiliki berbagai aplikasi tidak hanya dalam berbagai cabang matematika tetapi juga dalam fisika, ekonomi, teknik, statistik, dan ekonomi. Jadi, pemecah matriks memiliki manfaat aktualnya saat ini.

Bagaimana Kalkulator Matriks Mengalikan Persamaan Matriks

Mari kita mulai mengetahui cara kerja kalkulator perkalian matriks. Pertama saya akan memberi tahu Anda tentang ukuran setiap matriks karena tidak setiap matriks dapat dikalikan dengan matriks lain. Jadi, mari kita lihat ukuran matriks pertama ini yang memiliki 2 baris dan 3 kolom dan matriks yang kedua memiliki 3 baris dan 3 kolom. Jadi matriks pertama adalah matriks dua kali tiga. Jika kita lihat matriks kedua, itu adalah matriks tiga kali tiga. Jadi, untuk mengalikan dua matriks, kolom pada matriks pertama harus sama dengan baris pada matriks kedua.

$$\left[\begin{matrix} 2 & 3 & 1 \\ 2 & -7 & 4 \\ \end{matrix}\right].\left[\begin{matrix} 3 & 4 & 5 \\ 1 & 1 & 4 \\ 2 & 1 & 4 \\ \end{matrix}\right]$$

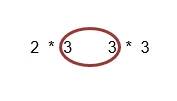
Kedua nomor dalam ini harus sama. Jika kedua bilangan ini tidak sama, Anda tidak dapat mengalikan kedua matriks. Jadi, pastikan angka-angka ini sama, sebelum mengalikan matriks. Angka luar memberi Anda ukuran matriks baru setelah Anda melakukan perkalian. Di sini bilangan luarnya adalah 2 dan 3, jadi ukuran matriks yang baru adalah matriks 2 kali 3.

Sekarang mari kita mulai, apa yang sebenarnya kita lakukan saat kita mengalikan dua matriks. Kami akan mengalikan baris dari matriks pertama dengan kolom dari yang kedua

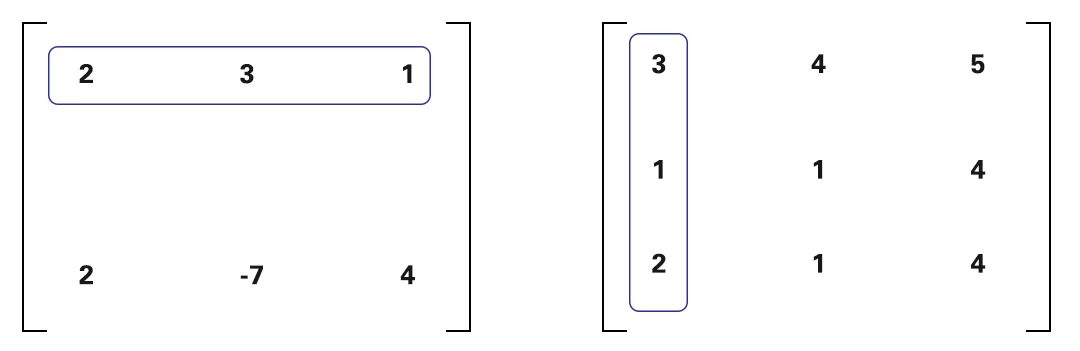
$$\left[\begin{matrix} 2 & 3 & 1 \\ 2 & -7 & 4 \\ \end{matrix}\right].\left[\begin{matrix} 3 & 4 & 5 \\ 1 & 1 & 4 \\ 2 & 1 & 4 \\ \end{matrix}\right]$$

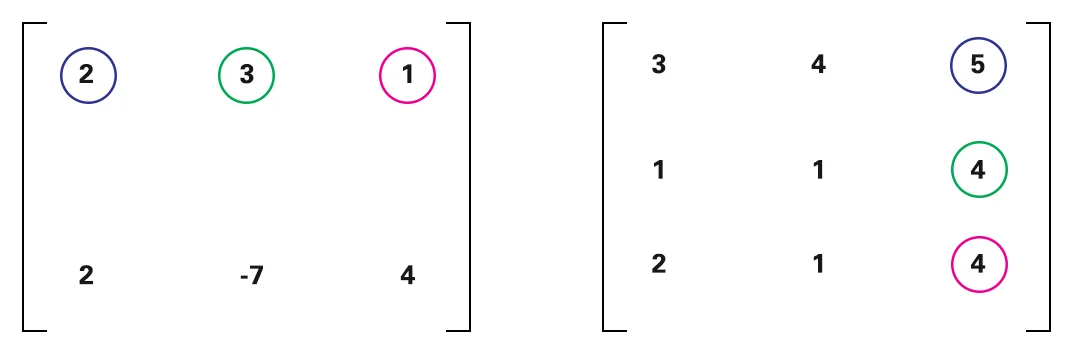
Kami akan mengalikan 2 dari matriks pertama dengan 3 dari matriks ke-2 dan seterusnya. Saya tandai dengan warna yang sama agar mudah dimengerti.

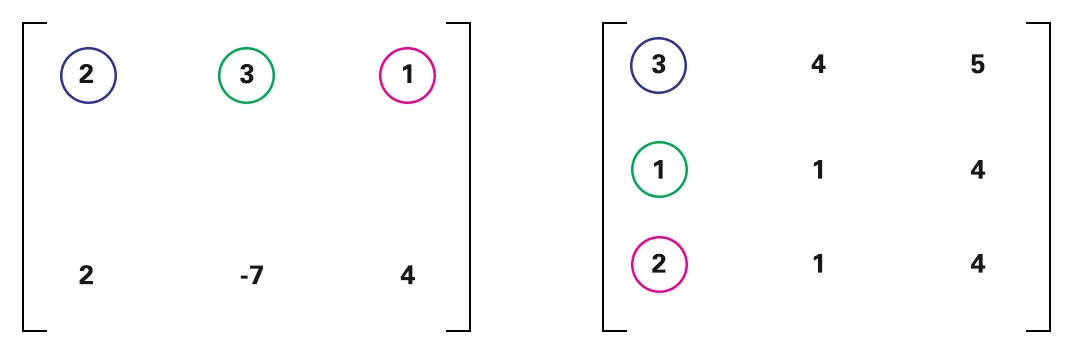
Kalikan kolom berikutnya dengan baris yang sama.

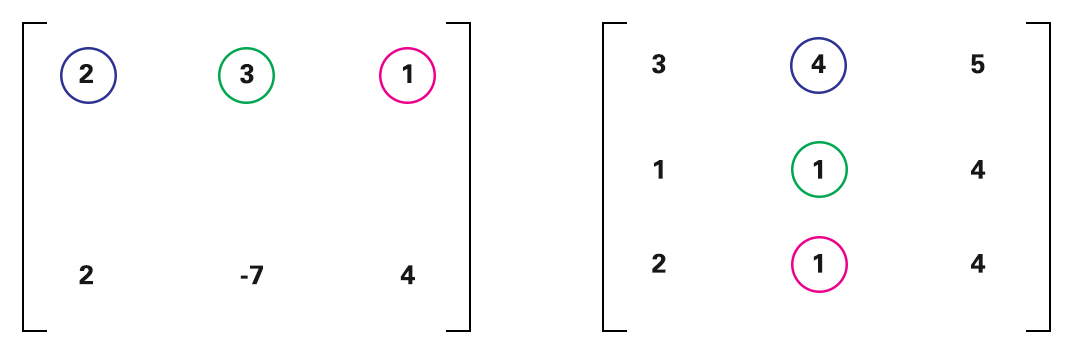
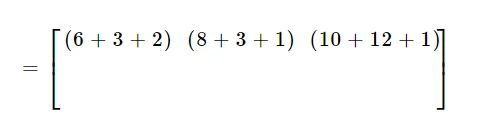
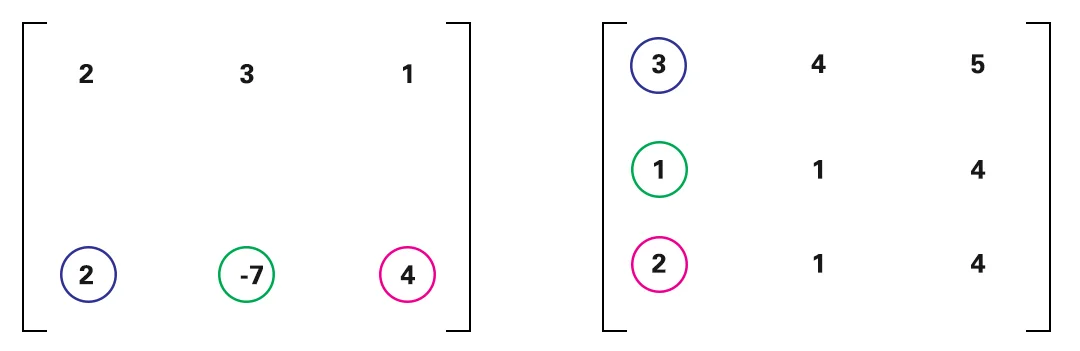
Setelah itu, lakukan perkalian baris ke-2 dari matriks pertama dengan semua kolom dari matriks ke-2.

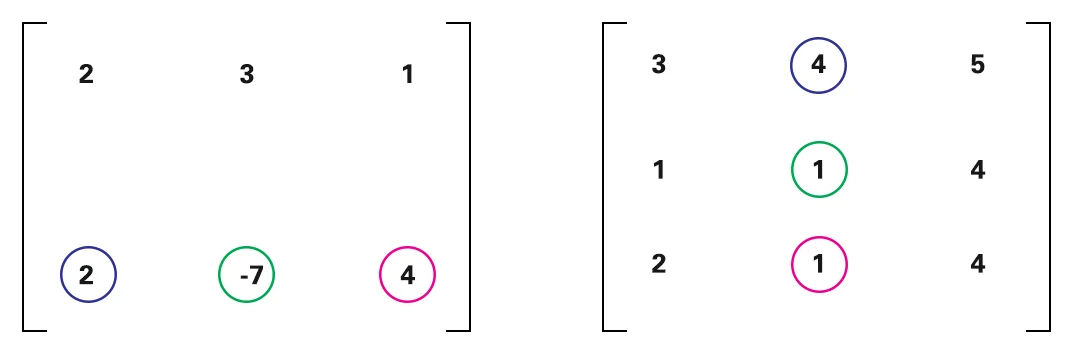
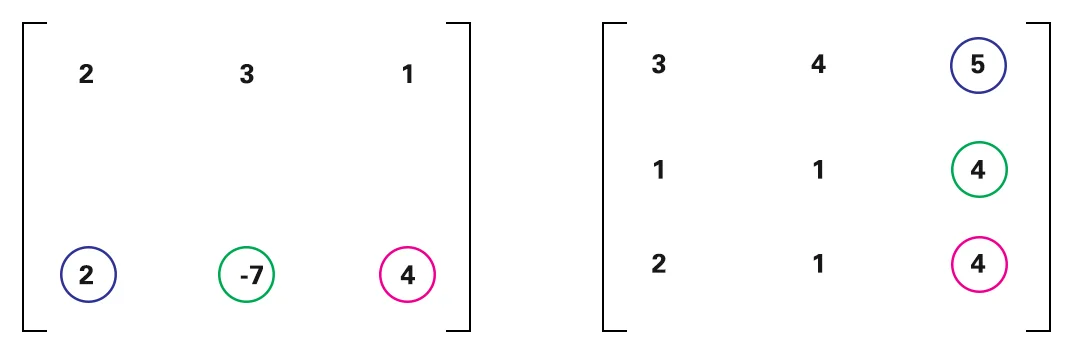
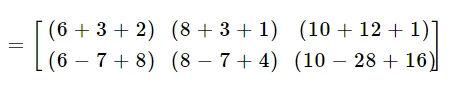
Akhirnya,

$$=\left[\begin{matrix}11& 12& 26\\7&5&-2 \end{matrix}\right]$$

Kalkulator Matriks Terbalik

Dalam matriks A adalah * n, saya juga merupakan matriks * n, dalam situasi ini matriks n * n B. Ini akan dilambangkan sebagai B = A^-1 dan akan dikatakan sebagai matriks invers (AA^-1 = A^-1). Matriks terbalik dilambangkan dengan A^-1.

Untuk mendapatkan matriks invers A dimana A^-1 ada, kalkulator matriks invers melakukan langkah-langkah berikut. Pertama-tama, bentuk matriks augmented [A / I] di mana I adalah matriks identitas n * n. Kemudian, untuk mendapatkan matriks [I / B], lakukan transformasi baris pada [A / I]. Sebenarnya di sini, matriks B adalah A^-1. Pada langkah terakhir, verifikasi dengan menunjukkan bahwa matriks ini sama satu sama lain, mis. B.A = A.B = I.

Satu hal yang harus diperhatikan bahwa setiap matriks tidak memiliki invers melainkan hanya matriks persegi. Tidak perlu setiap matriks memiliki invers. Dan itu adalah properti khusus dari matriks invers yang unik tetapi jika ada. Setiap matriks tidak memiliki lebih dari satu matriks.