Calculadora de matrices

Introducción-a-la-calculadora-matricial

Hoy discutiremos el funcionamiento de Matrix Calculator. Las matemáticas matriciales son en realidad una colección de elementos, dispuestos en filas y columnas y la combinación de ecuaciones lineales. En matemáticas matriciales,

los números 1, 2, 3, 4,… ..n

se denominan entradas o elementos de la matriz. Matriz representada por los siguientes símbolos (), [], || ||, por ejemplo.

$$\left[\begin{matrix} 2 & 1 & 3 \\ 4 & 2 & 1 \\ 3 & 3 & 2 \\ \end{matrix}\right] 3*3 $$

Hay muchos tipos de matrices, por ejemplo; matriz de fila, matriz de columna, matriz cuadrada, matriz nula, matriz identidad, matriz diagonal, matriz escalar, matriz triangular, matriz de transposición, matriz simétrica, matriz sesgada, matriz igual, matriz algebraica. Ahora sabremos cómo realiza su función la calculadora matricial.

Sin duda, las matrices tienen diversas aplicaciones no solo en diferentes ramas de las matemáticas sino también en física, economía, ingeniería, estadística y economía. Entonces, la calculadora de igualdad matricial tiene sus beneficios reales hoy en día.

Cómo la calculadora de matrices multiplica las ecuaciones de matrices

Comencemos a conocer el funcionamiento de la calculadora matricial simétrica. Primero le haré saber sobre los tamaños de cada matriz porque no todas las matrices se pueden multiplicar por otra matriz. Entonces, echemos un vistazo al tamaño de esta primera matriz que tiene 2 filas y 3 columnas y la segunda matriz tiene 3 filas y 3 columnas.

Entonces, la primera matriz es una matriz de dos por tres. Si echamos un vistazo a la segunda matriz, es una matriz de tres por tres. Entonces, para multiplicar dos matrices juntas, las columnas en las primeras matrices deben ser iguales a las filas en la segunda matriz.

$$\left[\begin{matrix} 2 & 3& 1\\ 2& -7;& 4\\ \end{matrix}\right].\left[\begin{matrix} 3& 4& 5\\ 1& 1& 4\\ 2& 1& 4\\ \end{matrix}\right]$$

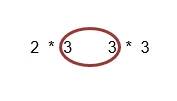
Estos dos números interiores deben ser iguales. Si estos dos números no son iguales, la calculadora simétrica no puede multiplicar las dos matrices. Por lo tanto, asegúrese de que estos números sean los mismos, antes de multiplicar matrices. Los números externos le dan el tamaño de la nueva matriz después de haber hecho la multiplicación. Aquí los números externos son 2 y 3, por lo que el nuevo tamaño de la matriz será una matriz de 2 por 3.

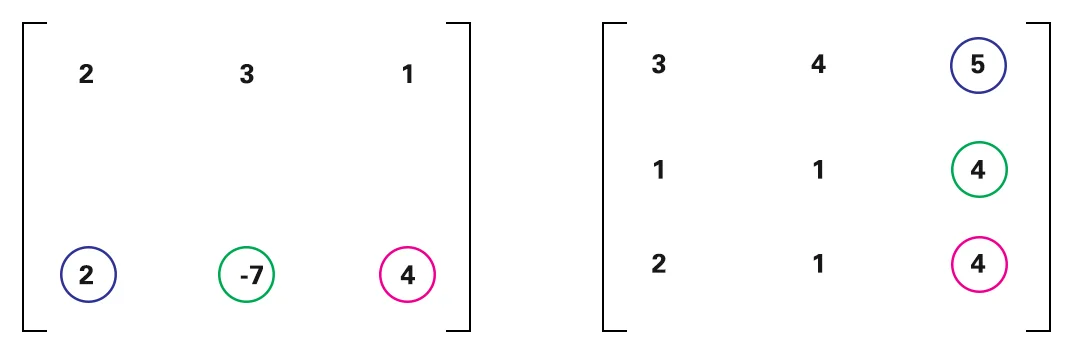
Ahora comencemos, lo que realmente hacemos cuando multiplicamos dos matrices. Multiplicaremos las filas de la primera matriz por las columnas de la segunda.

$$\left[\begin{matrix} 2 & 3& 1\\ 2& -7& 4\\ \end{matrix}\right].\left[\begin{matrix} 3& 4& 5\\ 1& 1& 4\\ 2& 1& 4\\ \end{matrix}\right]$$

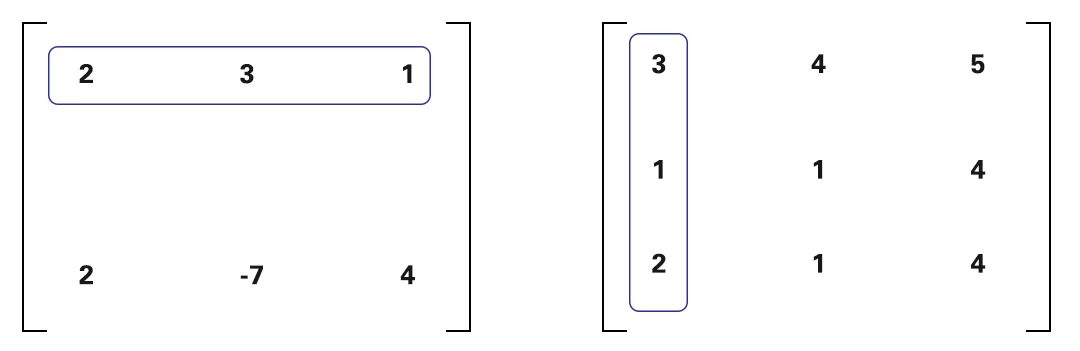
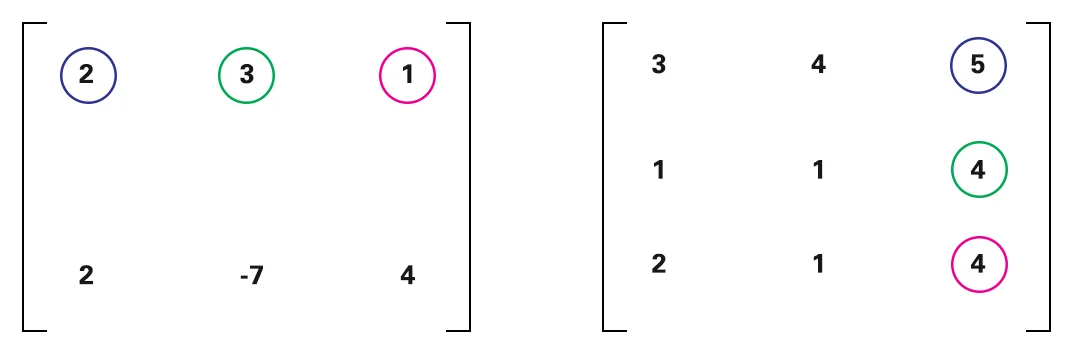
La calculadora de matriz simétrica sesgada multiplicará 2 de la primera matriz por 3 de la segunda matriz y así sucesivamente. Los resaltamos con el mismo color para que sea más fácil de entender.

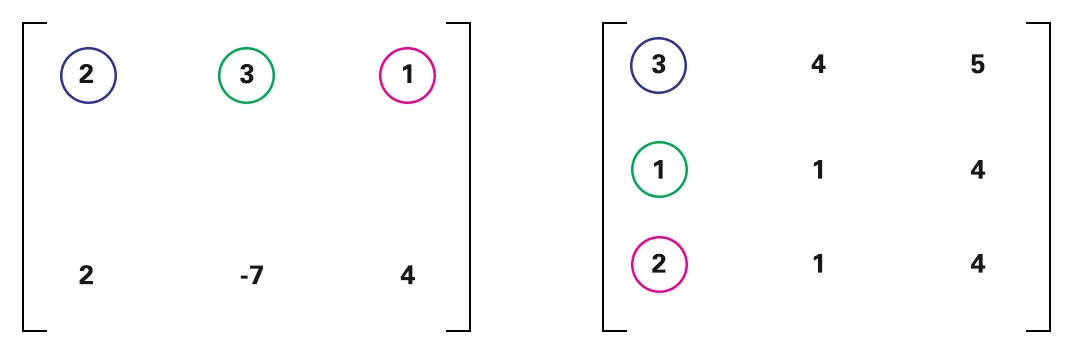
La calculadora simétrica matricial multiplicará las siguientes columnas con la misma fila.

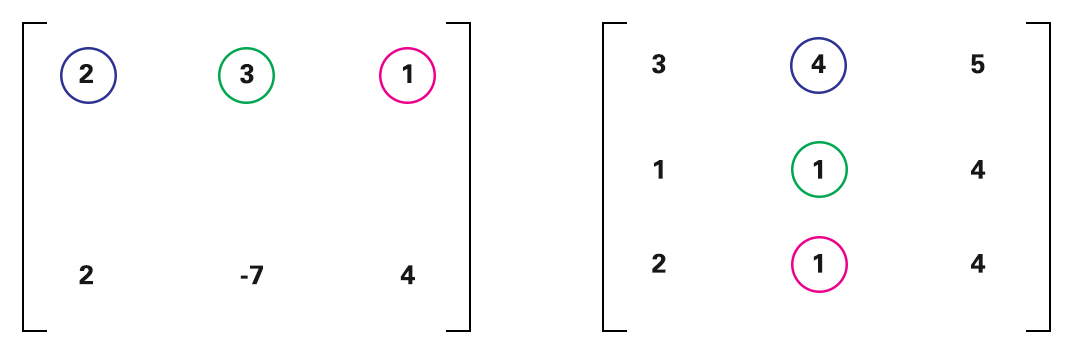
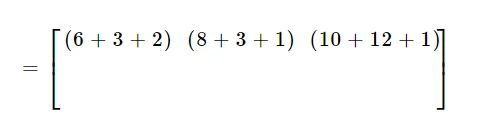
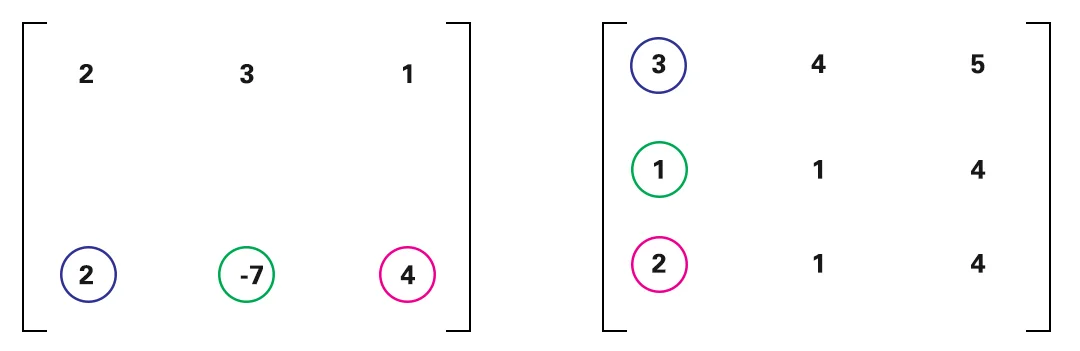
Después de eso, aplica la multiplicación a la segunda fila de la primera matriz con todas las columnas de la segunda matriz.

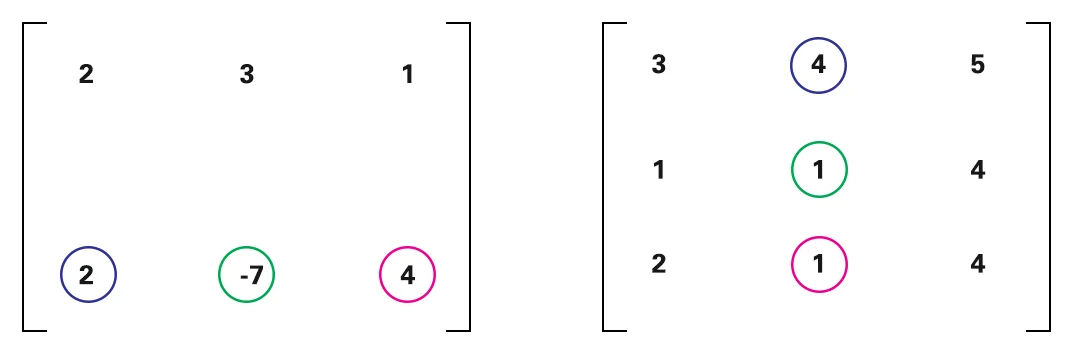
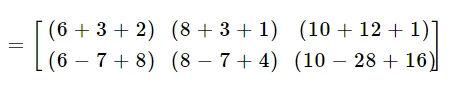
Finalmente,

$$=\left[\begin{matrix}11& 12& 26\\7&5&-2 \end{matrix}\right]$$

Así es como la calculadora de matriz simétrica sesgada funciona de manera eficiente para calcular los resultados.

Con su aprendizaje sobre la multiplicación de matrices, también puede aprender sobre los cálculos de factor y cómo calcular factorial usando la calculadora factorial.

Calculadora de multiplicación de matrices

En una A es una matriz * n, I también una matriz * n, en esta situación la matriz n * n B. Se denotará como B = A-1 y se dirá como una matriz inversa (AA-1 = A-1 A = I). La matriz inversa se denota por A-1.

Para obtener la matriz A inversa para la que existe A-1, la calculadora de multiplicación de matrices realiza los siguientes pasos. En primer lugar, forme una matriz aumentada [A / I] en la que I es una matriz identidad n * n. Luego, para obtener una matriz [I / B], realice transformaciones de fila en [A / I]. En realidad, aquí, la matriz B es A-1. En el último paso, verifíquelo mostrando que estas matrices son iguales entre sí, p. B.A = A.B = I.

Una cosa debe tenerse en cuenta que todas las matrices no tienen inversas sino solo matrices cuadradas. No es necesario que cada matriz tenga una inversa. Y es una propiedad especial de una matriz inversa que es única, pero si existe. Cualquier matriz no tiene más de una matriz.

¿Cómo encontrar la mejor calculadora matricial?

Hay muchas calculadoras de productos matriciales para encontrar el producto matricial. Encontrará todas esas calculadoras de soluciones matriciales en línea, pero la clave es encontrar la mejor que calcule la matriz sin errores.

Calculatored tiene una tonelada de convertidores y calculadoras y la calculadora de productos matriciales es una de ellas. Puede utilizar nuestra calculadora de matriz simétrica gratis en línea, ya que proporciona resultados precisos.

¿Cómo usar la calculadora matricial?

Nuestra calculadora de producto matricial es la mejor calculadora para resolver un sistema de ecuaciones y no es difícil de usar. Solo necesita seguir esos pasos para calcular los resultados. Los pasos para usar la calculadora de solución matricial son los siguientes:

Paso # 1: Ingrese los valores de la matriz en la Fila 1

Paso # 2: Ingrese los valores de la segunda matriz en la Fila 2

Paso # 3: Seleccione si desea calcular la matriz inversa o la matriz 2 * 2

Paso # 4: haga clic en el botón de búsqueda

Al instante, después de hacer clic en el botón, nuestra calculadora de solución matricial le mostrará instantáneamente los resultados precisos.