Calculadora Matricial

Hoje vamos discutir o funcionamento da Calculadora de Matriz. Matemática matricial é na verdade uma coleção de elementos, dispostos em linhas e colunas e a combinação de equações lineares. Na matemática da matriz,

são chamados de entradas ou elementos da matriz. Matriz representada pelos seguintes símbolos (), [], || ||, por exemplo,

$$\left[\begin{matrix} 2 1 3 \\ 4 2 1 \\ 3 3 2 \\ \end{matrix}\right] 3*3 $$

Existem muitos tipos de uma matriz, por exemplo; matriz de linha, matriz de coluna, matriz quadrada, matriz nula, matriz identidade, matriz diagonal, matriz escalar, matriz triangular, matriz transposta, matriz simétrica, matriz oblíqua, matriz igual, matriz algébrica. Agora saberemos como a calculadora de matrizes executa sua função. Sem dúvida, as matrizes têm várias aplicações, não apenas em diferentes ramos da matemática, mas também na física, economia, engenharia, estatística e economia. Então, o solucionador de matriz tem seus benefícios reais hoje em dia.

Como a calculadora de matrizes multiplica as equações das matrizes

Vamos começar a conhecer o funcionamento da calculadora de multiplicação de matrizes. Em primeiro lugar, vou informá-lo sobre os tamanhos de cada matriz porque nem toda matriz pode ser multiplicada por outra matriz. Então, vamos dar uma olhada no tamanho desta primeira matriz que tem 2 linhas e 3 colunas e a segunda matriz tem 3 linhas e 3 colunas. Portanto, a primeira matriz é uma matriz dois por três. Se dermos uma olhada na segunda matriz, é uma matriz três por três. Portanto, para multiplicar duas matrizes, as colunas das primeiras matrizes devem ser iguais às linhas da segunda matriz.

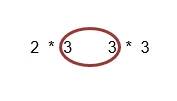
Esses dois números internos devem ser iguais. Se esses dois números não forem iguais, você não pode multiplicar as duas matrizes. Portanto, certifique-se de que esses números são iguais, antes de multiplicar as matrizes. Os números externos fornecem o tamanho da nova matriz após a multiplicação. Aqui, os números externos são 2 e 3, então o novo tamanho da matriz será 2 por 3 da matriz.

Agora vamos começar, o que realmente fazemos quando multiplicamos duas matrizes. Vamos multiplicar as linhas da primeira matriz pelas colunas da segunda

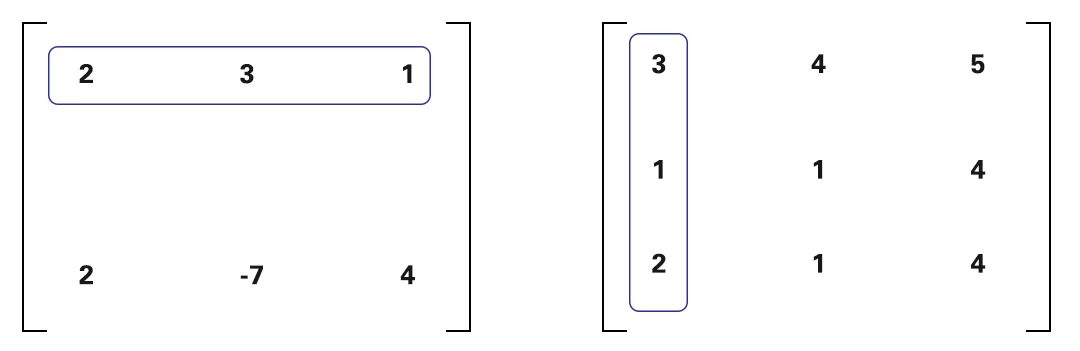
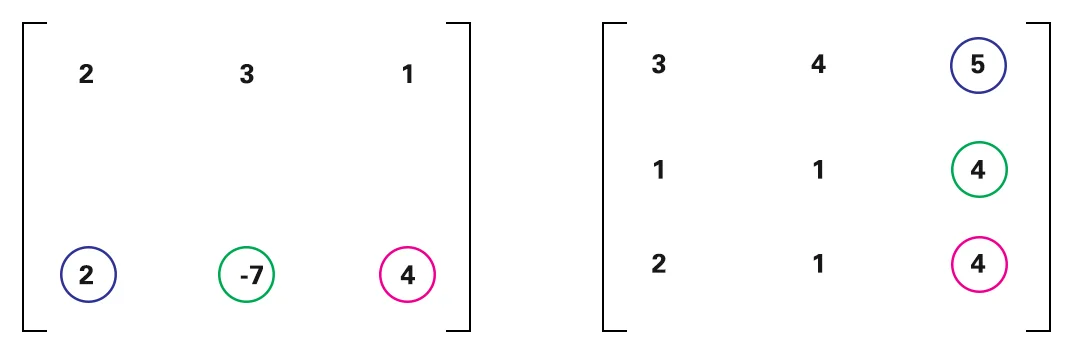
$$\left[\begin{matrix} 2 3 1 \\ 2 -7 4 \\ \end{matrix}\right].\left[\begin{matrix} 3 4 5 \\ 1 1 4 \\ 2 1 4 \\ \end{matrix}\right]$$

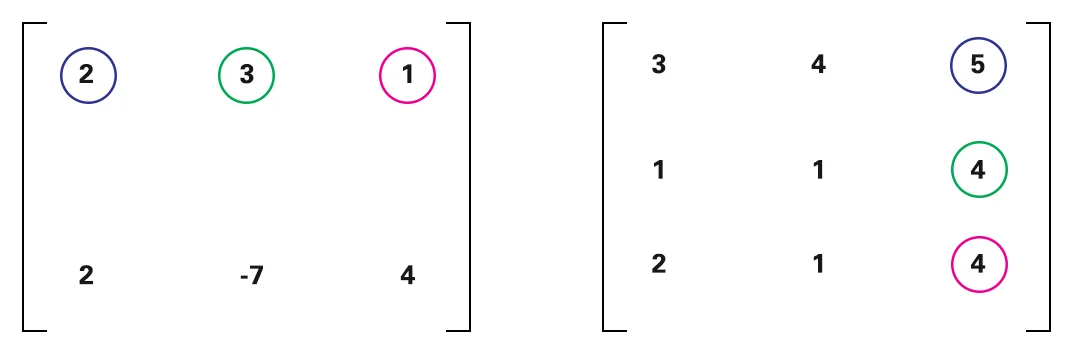
Multiplicaremos 2 da primeira matriz por 3 da 2ª matriz e assim por diante. Eu os destaquei com a mesma cor para facilitar o entendimento.

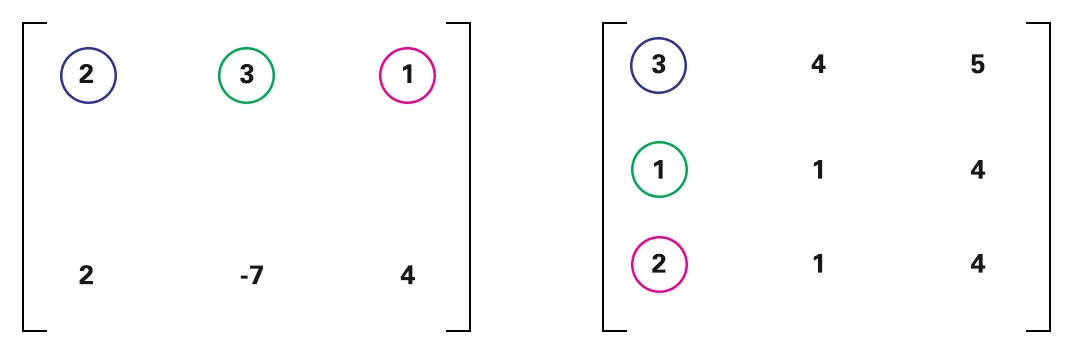
Multiplique as próximas colunas com a mesma linha.

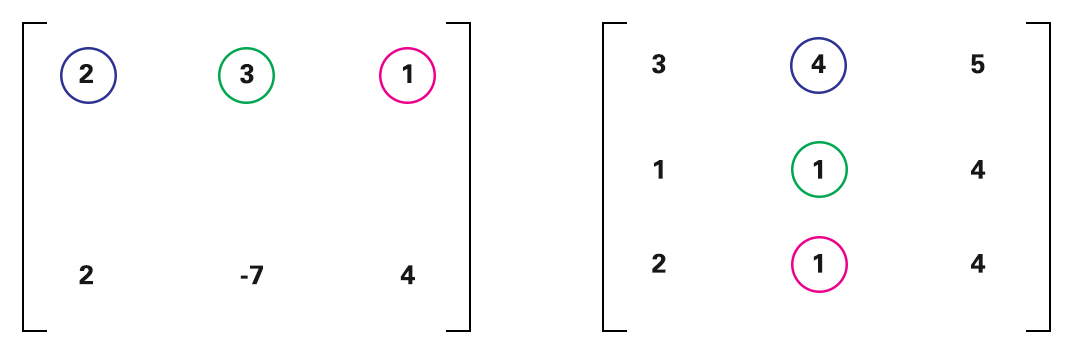
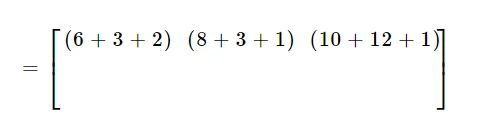
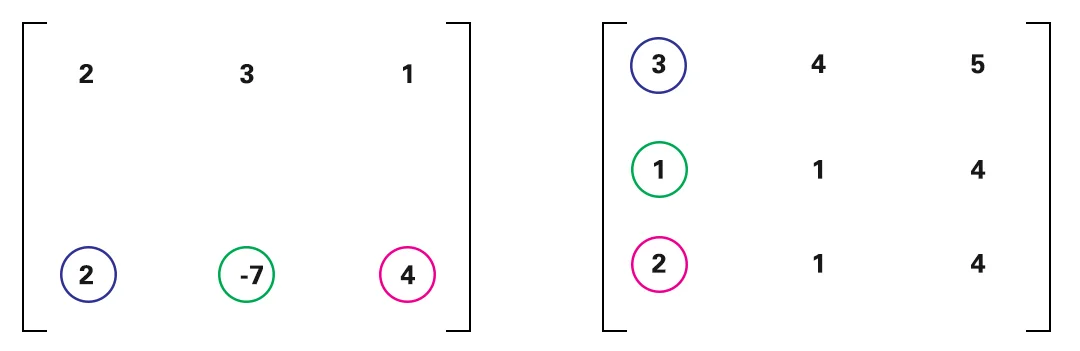
Depois disso, aplique a multiplicação para a 2nd linha da primeira matriz com todas as colunas da 2nd matriz.

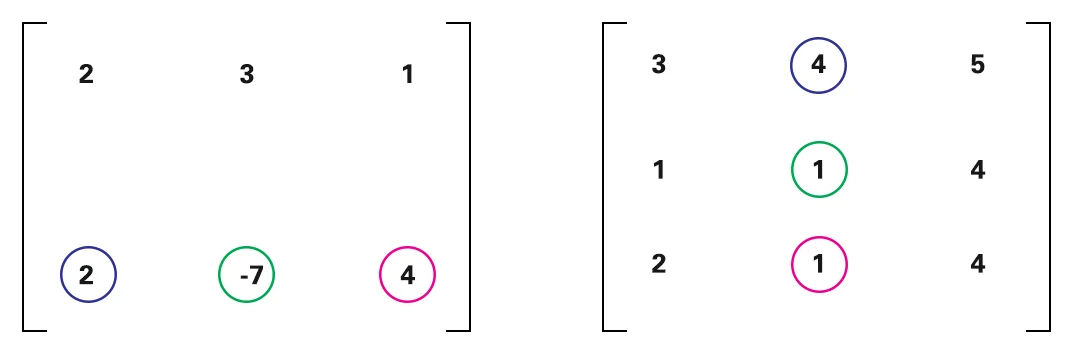
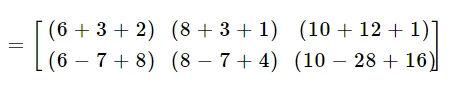
Finalmente,

$$=\left[\begin{matrix}11 12 26\\7 5 -2\end{matrix}\right]$$

Calculadora de matriz inversa

Em um A é uma matriz * n, I também uma matriz * n, nesta situação a matriz n * n B. Ela será denotada como B = A^-1 e será dita como uma matriz inversa (AA^-1 = A^-1 A = I). A matriz inversa é denotada por A-1.

Para obter a matriz inversa A para a qual A^-1 existe, a calculadora de matriz inversa executa as seguintes etapas. Em primeiro lugar, forme uma matriz aumentada [A / I] na qual I é uma matriz de identidade n * n. Então, para obter uma matriz [I / B], execute transformações de linha em [A / I]. Na verdade, aqui, a matriz B é A^-1. Na última etapa, verifique-o mostrando que essas matrizes são iguais entre si, por exemplo, B.A = A.B = I.

Uma coisa deve ser notada que toda matriz não possui inversos, mas apenas matrizes quadradas. Não é necessário que toda matriz tenha uma inversa. E é a propriedade especial de uma matriz inversa que ela é única, mas se existir. Qualquer matriz não possui mais do que uma matriz.