Calculadora Integral

Definição Integral

De acordo com a definição integral, é a atribuição de números para definir e descrever a área, volume, deslocamento e outros conceitos. No cálculo, a integração é a operação mais importante junto com a diferenciação.

O que é integração?

A integração é usada para encontrar a equação diferencial de um integral ou integrais. Ele produz uma função para diferenciar e calcular a área sob a curva de um gráfico da função.

A definição integral é usada para encontrar áreas, pontos centrais, volumes, etc. A calculadora de integração é usada para definir integral para encontrar a área sob a curva como esta:

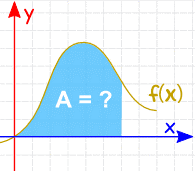
Onde,

F(x) é a função e

A é a área sob a curva.

Clique em para aprender a fórmula e os cálculos de Variância e Covariância.

O que é Integrand?

É uma função que deve ser integrada denominada Integrand. Em uma equação integral ou fórmula de integração, é denotado como a função f (x).

O que é notação integral?

Para uma equação integral

$$∫2xdx$$

∫ é o símbolo integral e 2x é a função que queremos integrar.

Nesta equação integral, dx é o diferencial da Variável x que destaca que a variável de Integração é x. O dx mostra a direção ao longo do eixo x e dy mostra a direção ao longo do eixo y.

Símbolo integral e regras integrais são usados pela calculadora de integrais para obter resultados rapidamente. 

Como calcular o Integral?

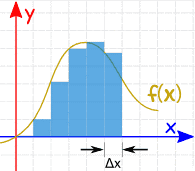
Podemos calcular a função em algumas etapas simples, primeiro dividir a área em fatias e somar a largura dessas fatias de Δx. Então a resposta não será precisa. (veja a figura 1)

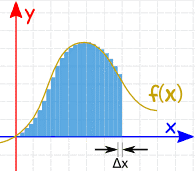
Se fizermos muito Δx com largura menor e somarmos todas essas pequenas fatias, a precisão da resposta ficará melhor. (veja a figura 2)

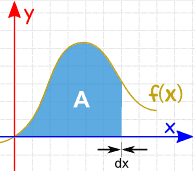
Se a largura das fatias se aproximar de zero, a resposta se aproxima do resultado verdadeiro ou real. assim,

We now say that dx to mean the Δx slices are approaching zero in width.

Observe que a integral é o inverso da derivada

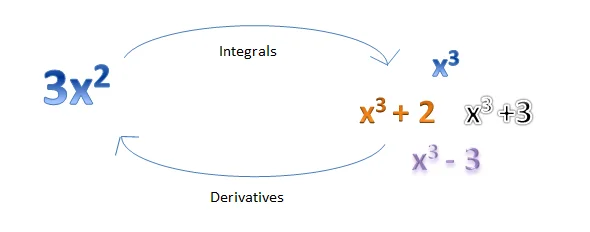
O que é Indefinite Integral?

A integral indefinida não possui o limite superior e o limite inferior da função f (x). A integral indefinida também é conhecida como antiderivada

Use nossa calculadora integral indefinida para resolver valores definidos e indefinidos. 

O que é Double Integral?

Integral duplo tem 2 variáveis. Considere f (x, y) como uma função em um espaço 3D no plano xy e R como qualquer região no plano xy. Se dividirmos a região R em sub-regiões menores e δAi = δxi δyi ser a área de sua sub-região.

Então, a integral dupla de f (x, y) sobre a região R pode ser definida como:

ʃʃR ƒ (x, y) dxdy = limn ͢ 0 Σ (n, i = 1) ƒ (xi, yi) δxi δyi

onde (xi, yi) é qualquer ponto na i-ésima sub-região

Use a calculadora da área do trapézio e a calculadora da área do retângulo para fortalecer ainda mais seus conceitos matemáticos relacionados à área e à superfície.

Fórmulas Integrais Duplas

Abaixo estão as fórmulas integrais duplas com diferentes funcionalidades, mas além dessas fórmulas também pode-se tentar a calculadora de integral dupla online:

p>If f (x, y) ≥0 in a region R and S⊂R:
∬Sf (x, y) dA≤ ∬Rf (x, y) dA

• Para encontrar o integral duplo da soma de duas funções:
  ∬R [f (x, y) +g (x, y)] dA= ∬Rf (x, y) dA +∬Rg (x, y) dA

• Para encontrar a integral dupla da diferença de duas funções:
  ∬R [f (x, y) −g (x, y)] dA= ∬Rf (x, y) dA −∬Rg (x, y) dA

• No caso de um fator constante:
  ∬Rkf (x, y) dA= k∬Rf (x, y) dA

• For f (i, n) ≤ g (x, y) in R:
  Rf (x, y) dA≤ ∬Rg (x, y) dA

• Para encontrar o volume de um sólido:
  V=∬Rf (x, y) dA

• Para encontrar o volume do sólido entre duas superfícies:
  If f (x, y) ≥ g (x, y) over a region R, then:
  V=∬R [f (x, y) −g (x, y)] dA

Como calcular os integrais duplos?

Uma dificuldade no cálculo de integrais duplos é determinar os limites da integração. Os limites de integração como ordem dxdydxdy são necessários para determinar os limites de integração para a ordem dydxdydx integral equivalente.

Em integrais duplos, o processo de alternar entre a ordem dxdydxdy e a ordem dydxdydx é chamado de alteração da ordem de integração. A calculadora de integral dupla ajuda você a obter resultados precisos.

Como usar a calculadora de integral passo a passo?

Nossa calculadora de integrais indefinidas é a melhor calculadora de integral passo a passo.

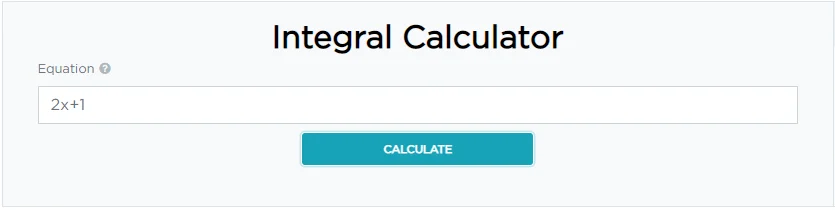
Basta inserir sua equação como 2x + 1

Pressione o botão "CALCULAR" e a Calculadora Integral indefinida a Integral da função passo a passo. Você também pode verificar esses passos com nossa melhor calculadora de integral indefinida.