Summation Formulas to Undertand How to Solve Sigma Notation?
In this article, you will learn about summation formulas. You will also understand how to calculate the sum of a series using this formula.
What is Summation?
The process of finding the sum of a set of numbers is called summation. It represents the larger sum of a series in a short form and is denoted by sigma. Various types of summation are arithmetic sequence, geometric sequence etc.
The summation of sequences has two types of sequences known as a finite and infinite set of sequences. The finite sequence has finite numbers of elements, whereas the infinite sequence has undefined numbers without limit.
Summation Formula
The summation does not have a specific formula; many different summation formulas depend on the type of series. But the generalised summation formula in sigma notation is:


Series Summation Formulas
There are summation formulas to find the sum of the natural numbers, the sum of squares of natural numbers, the sum of cubes of natural numbers, the sum of even numbers, the sum of odd numbers, etc.
1. Sum of n Even numbers
If there are n number of even numbers, the sum formula will be,
$$ \sum_{i=1}^n \; 2x_i \;=\; 2 + 4 + 6 +\; ...\;+n \;=\; n(n+1) $$2. Sum of Odd numbers
If there are n odd numbers, the sum formula will be,
$$ \sum_{i=1}^n (2x_i \;+\; 1) \;=\; 1 + 3 + 5 +\;...\;+n \;=\; n^2 $$3. Sum of n Natural numbers
The summation formula to find sum of first n natural numbers is,
$$ \sum_{i=1}^n \; x_i \;=\; 1 + 2 + 3 + \; ... \; +n \;=\; \frac {n(n+1)} {2} $$4. Sum of Squares
The summation formula to calculate sum of squares of the first n natural numbers is,
$$ \sum_{i=1}^n \; x_i^2 \;=\; 1^2 + 2^2 + 3^2 + \;...\; + n^2 \;=\; \frac {n(n+1)(2n+1)} {6} $$5. Sum of Cubes
The summation formula to find sum of cubes of n natural numbers is,
$$ \sum_{i=1}^n \; x_i^3 \;=\; 1^3 + 2^3 + 3^3 + \;...\; +n^3\;=\; \frac {n^2(n+1)^2} {4} $$6. Sum of Fourth power
To calculate sum of n numbers having 4th power is,
$$ \sum_{i=1}^n \; x_i^4 \;=\; 1^4 + 2^4 + 3^4 +\;...\; + n^4 \;=\; \frac {n(n+1)(2n+1)(3n^2 + 3n - 1)} {30} $$How to Solve Sigma Notation?
Suppose we have a series of n terms such that xn= x1,x 2,x 3,…. We can calculate the sum of this series by using the follow summation formula,
$$ \sum_{i=1}^N \; x_i \;=\; x_1 + x_2 + x_3 +\; .....\; + X_n $$It means that the sum of a series can be calculated by adding all its terms together. Here we are providing you a step-by-step method of calculating the sum of series of any number. Follow the given steps.
- Identify the upper and lower limit of the series.
- Write the series in the form of sigma notation formula.
- Calculate the sum by adding all consecutive terms of the series.
Let’s see the following examples to understand how the sum is calculated by summation formulas.


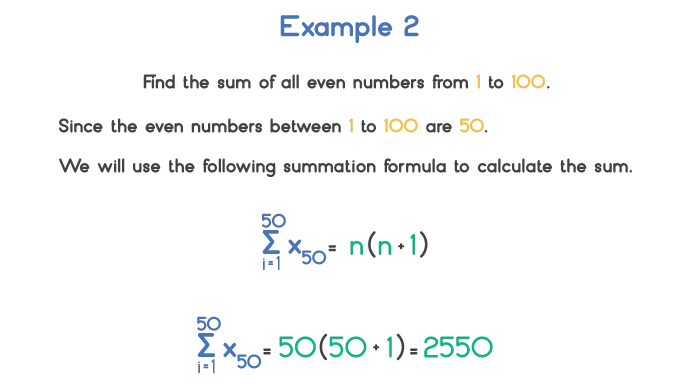
Related Formulas
The formulas related to summation formula are:
- Arithmetic Mean: $$ A.M \;=\; \frac {\sum_{i=1}^n a_i}{n} $$
- Geometric Mean $$ G.M \;=\; \sqrt n{x_1 * x_2 * x_3 *...* x_n} $$
FAQ’s on Sigma Notation Formulas
What is the Σ in Maths?
It is the sign of summation that adds up all numbers of the sequence. It is used in summation formula that is,
$$ \sum_{i=1}^n \; x_i \;=\; x_1 + x_2 + x_3 +\; .....\; + x_n $$What is the Summation Formula of Natural Numbers?
If there is n natural numbers then the summation formula will be,
$$ \sum_{i=1}^n x \;=\; \frac{n(n+1)}{2} $$

