Log Formula - Rules to Solve The Logarithm Equations with Examples

Introduction

In this article, you will learn what is logarithm. You will also understand how to solve logarithmic equations.

What is Logarithm?

The logarithm is used to find the inverse of exponential and multi-valued functions. It is an exponent to which a base must be raised to obtain the required number. It helps to solve many physical phenomena.

The log and anti log are widely used in mathematical analysis to solve different problems. The log of a number has two parts, the mantissa and the characteristic part.

Mantissa

It is the decimal portion of a natural logarithm formula. It is always positive; if it is not positive, we must convert it into a positive number.

Characteristic

It is the entire portion of a number before the decimal point. If it is less than one, the characteristic is negative, and the zeros are written before the decimal. The number of zeros is written on the right side if it is more significant than one.

Log Formula

The log formula is the exponential form of a number. Mathematically, if x is the logarithm of n to the base b, we can write it as:

$$ b^x \;=\; n In the term of logarithm,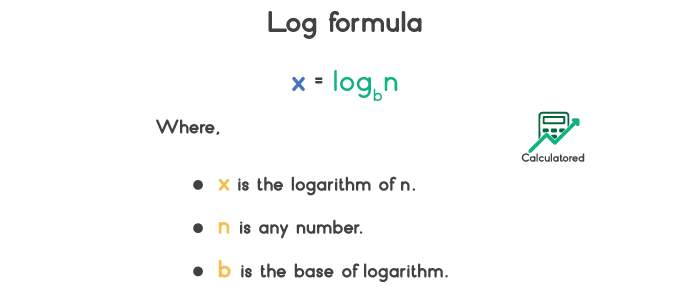

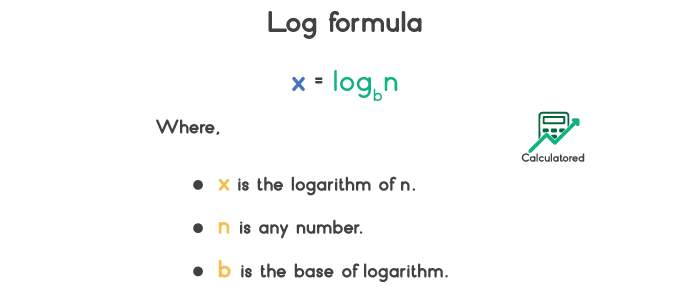
How to Solve Logarithmic Equations?

The log equations can be solved easily by using the logarithm laws. To write a number in terms of a logarithm equation, you can use the following steps.

1. Simplify the logarithm equation by using logarithm laws.
2. Write the number in exponent form.
$$ b^x \;=\; n $$
3. Apply the log on both side such that,
$$ x \;=\; \log_b n $$
4. If you have a number in decimals, use the logarithm table to find log.

For example,

If we have, 2³ = 8

By using natural logarithm formula, $$ 8 \;=\; \log_2 3 $$

So the log of 8 to the base of 2.

The more detailed examples of logarithmic equations will discuss after the discussion of logarithmic equations rules.

Logarithm Rules and Examples

There are some important and basic rules to find the logarithm of a number. These are,

1. Product Rule of Log
$$ \log_b mn \;=\; \log_b m + \log_b n $$
2. Quotient Rule of Log
$$ \log_b \frac{m}{n} \;=\; \log_b m - \log_b n $$
3. Power Rule of Log
$$ \log_b n^p \;=\; p \log_b n $$
4. Roots Logarithmic Formula
$$ \log_b \sqrt[p] n \;=\; \frac{1}{p} \log_b n $$
5. Change of base Formula for Logarithms
$$ \log_b n \;=\; \log_a n \log_b a $$

Examples of Logarithmic Equations

Consider we have a logarithmic function log x = 10.23. Let's understand with the example how to find the value of x from this using logarithm formula. So let's understand the logarithm rules and examples in a below section.

Related Formulas

Antilog Formula

It is the inverse of the logarithm of a number to find the original number. The formula is:

Where,
n is the number.
b is the base of log.
x is the log value of n.

Frequently Asked Questions

What is the change of base formula for logarithms?

The change of base formula is used to change the base of a logarithm value. The formula is,

$$ \log_b n \;=\; \log_a n \; \log_b a $$

How to write logarithmic equations?

You can write a number as a logarithm equation easily. For example, to write n as the base of b, the log equation is,

$$ x \;=\; log_b n $$