Understand Geometric Sequence Formula to Find the nth term with Examples

In this article, you will learn what a geometric sequence formula is and how to find the sum of n terms of the sequence.

What is a Geometric Sequence?

A geometric sequence is a sequence of non-zero numbers where each term is calculated by multiplying the previous term by a fixed number. The fixed non-zero number is called the common ratio of the sequence. The geometric sequence is also known as geometric progression. For example, sequences 2, 6, 18, 54, … is a geometric sequence. It is obtained by multiplying three by each previous term. The common ratio can be calculated by dividing two consecutive terms.

Geometric Sequence Formula

The geometric sequence formulas include two different formulas, one is to find the nth term of the sequence, and the second is to find the sum of n terms. If there are n terms in a geometric sequence and r are the common ratio, then the geometric sequence is of the form,

a, ar, ar²,ar³,……

There are two types of geometric sequence formula for nth term.

1. The formula of nth term of the geometric sequence is,




2. If there are finite number of terms than the sum of n terms of the sequence formula is,

How to Find Geometric Sequence?

Suppose we have n terms of a geometric sequence and r is the common ratio then the sequence is a, ar, ar²,ar³,…… Then the sum of n terms of the sequence can be calculated as:

Or,

We can also calculate the terms of the geometric sequence by multiplying the common ratio to the previous terms. You can use the following steps to calculate geometric sequence.

1. Find the common ratio r by dividing two consecutive terms.
2. It there are finite terms in the sequence then to find sum of nth term, use the formula,
$$S_n\;=\;\frac{a\;(1\;-\;r^n)}{1\;-\;r}$$
3. If there are infinite terms, then use
$$S_n\;=\;\frac{a}{n\;-\;1}$$
4. If the nth term is unknown then the nth term can be calculated by,
$$a_n\;=\;ar^{n-1}$$

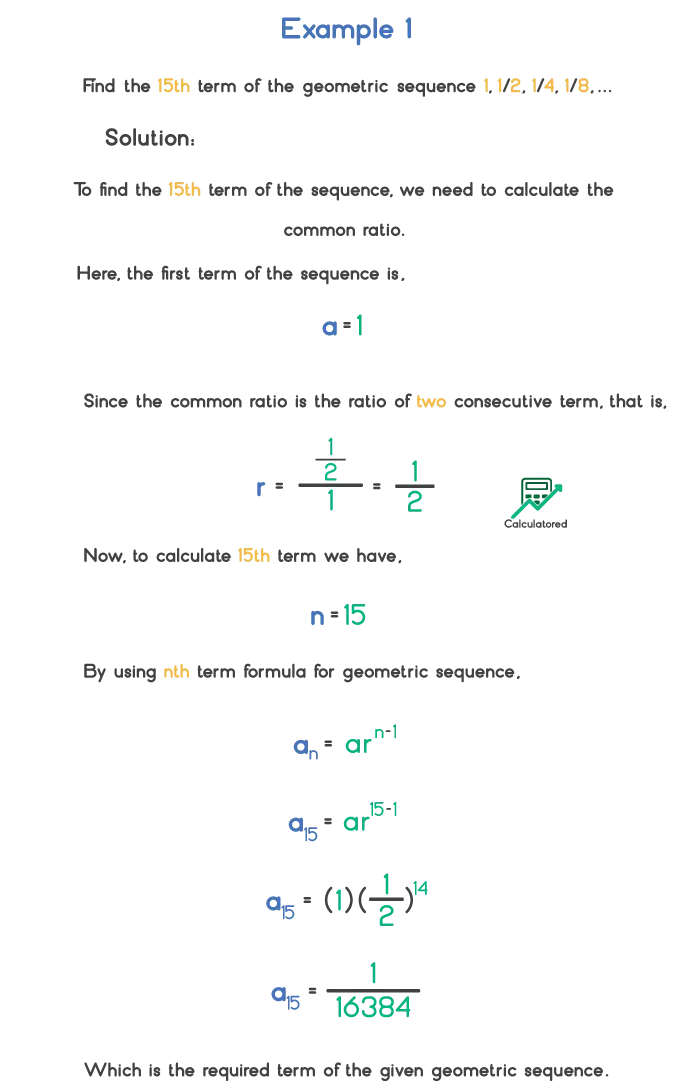
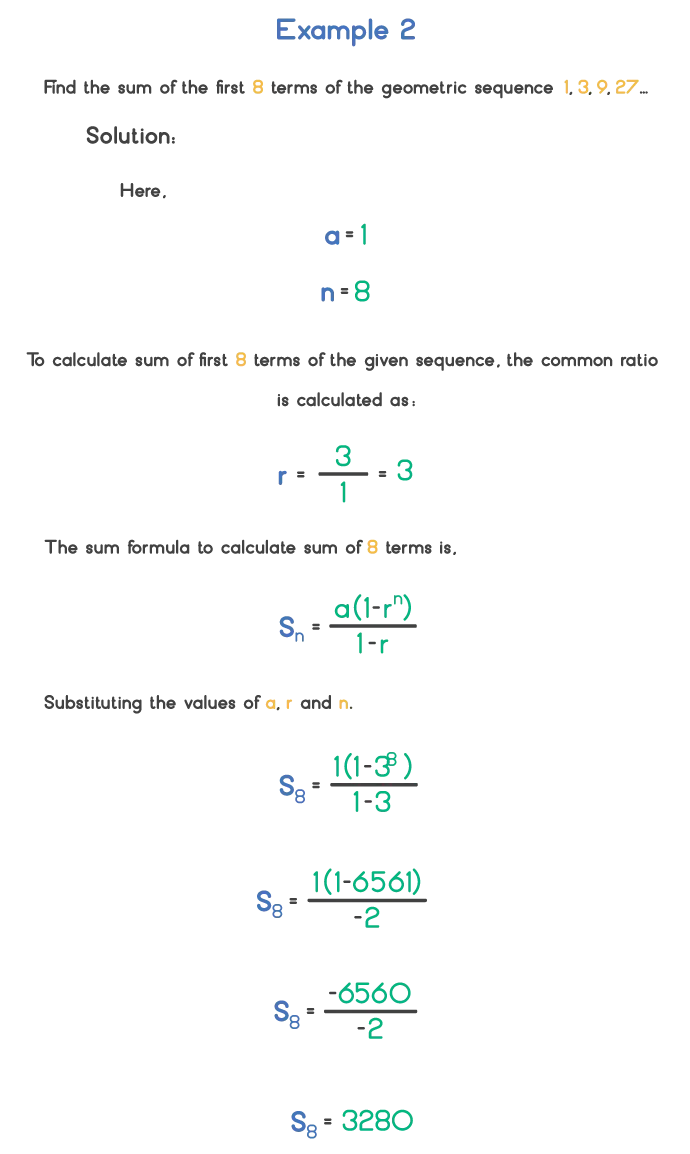
Let’s see the following examples to understand the nth term and the sum for a geometric sequence.

Related Formulas

• Arithmetic Sequence formula

The arithmetic sequence is a sequence in which there is a common difference between every consecutive term. All term of the sequence can be calculated by using the arithmetic sequence formula, which is,

$$a_n\;=\;a_1\;+\;(n\;-\;1)d$$

Where,

• a_n = is the nth term
• a₁ = first term of the sequence
• d = common difference
• Harmonic Sequence Formula

The harmonic sequence is a sequence of numbers such that there is a common difference between the reciprocals of any two consecutive terms. In other words, a harmonic sequence is formed by taking the reciprocals of every term in an arithmetic sequence. The harmonic sequence formula is,

$$a_n\;=\;\frac{1}{a\;+\;(n\;-\;1)d}$$

Where, a is the first term and d is the common difference between two consecutive terms.

FAQ’s

Why is it Called a Geometric Sequence?

The geometric series indicates that each term is the geometric mean of its two neighbouring terms. That’s why it is named as a geometric sequence that is formed by the geometric mean of two consecutive terms of a series.

What are the Characteristics of a Geometric Sequence?

In a geometric sequence.

• Each term is equal to the previous term times a constant.
• The non-zero multiplier is called the common factor.
• The geometric mean of two consecutive terms is the square root of their product.
• If the common ratio is greater than 1, infinite geometric sequences will approach positive infinity.
• If r is between 0 and 1, the sequences will approach zero.