Understand the Matrix Formula & Solve the Matrix With Example

Introduction

In this article, you will learn how to solve matrix equations. You will also learn how to find a matrix's adjoint, inverse, and determinant.

What is the Matrix?

A matrix is a set of numbers arranged in rows and columns to form a rectangular array. The entries of this set are called elements of the matrix. The size of the matrix is called the order of the matrix. It depends on its rows and columns.

If a matrix A has order m-by-n, having m rows and n columns, it can be expressed as:

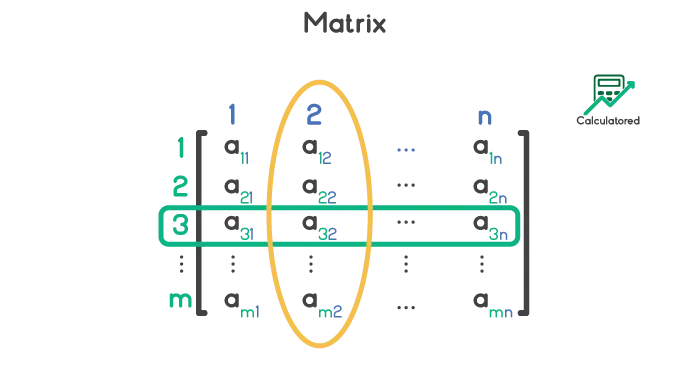
If the number of rows and columns of a matrix is the same i.e. 2-by-2, 3-by-3 or 4-by-4, the matrix is known as square matrix. Matrices have many applications not only in different branches of mathematics but also physics, engineering, statistics and economics.

Matrix Formula

It is a rectangular array of numbers that are arranged in rows and columns. There are different standard operations that are applied on matrices like addition, subtraction, multiplication etc. These are used to find specific matrices like adjoint, inverse and determinant.

To find these matrices, you can use the following formulas.

1. Adjoint Matrix Formula
2. Inverse Matrix Formula
3. Matrix Determinant formula

Adjoint Matrix Formula

The adjoint of a square matrix can be calculated by interchanging the diagonal elements and interchanging the signs of other entries. But the adjoint of a matrix of order greater than 2, is complex. It is calculated by finding transpose of cofactors of all entries.

Adjoint of a square matrix A of order 2 is,

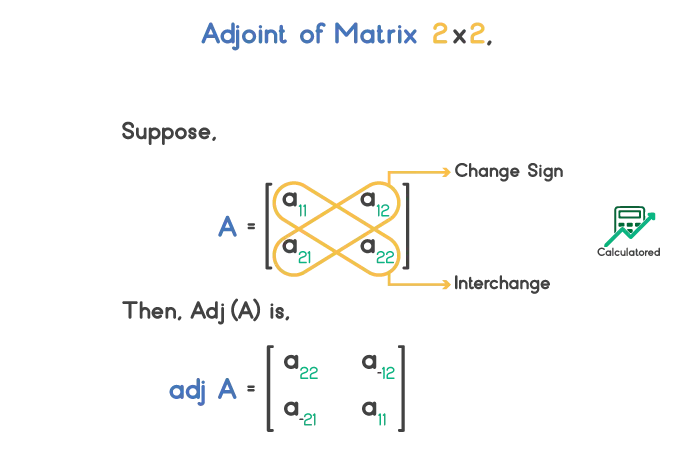
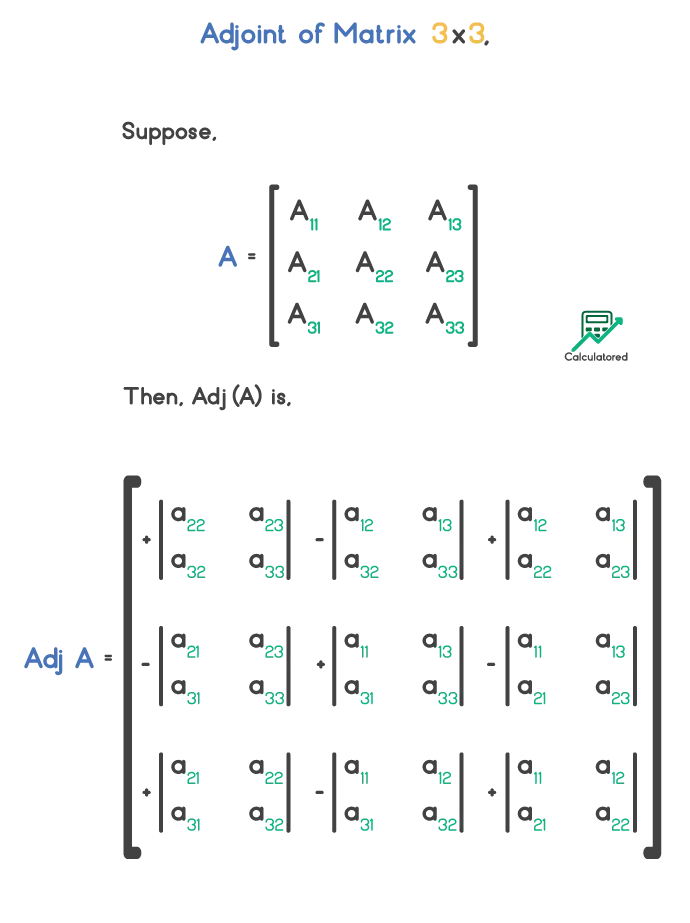
Adjoint of a matrix A of order greater than 2 is,

$$ Adj(A) \;=\; \begin{bmatrix} A_11 & A_12 & A_13 \\ A_21 & A_22 & A_23 \\ A_31 & A_32 & A_33 \\ \end{bmatrix} $$

It can be expressed as,

Inverse Matrix Formula

The inverse of a square matrix A is defined as the ratio of adjoint and modulus of A. The formula is:

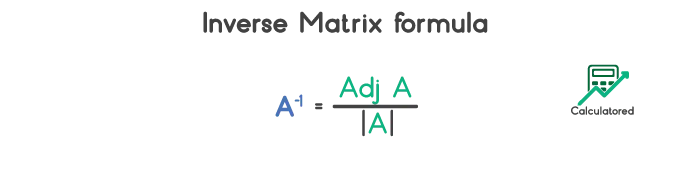
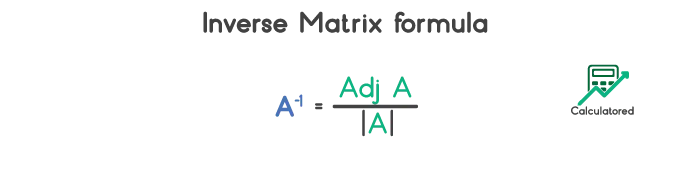
The inverse formula for a matrix of order greater than 2 is,

$$ A^{-1} \;=\; \frac{1}{|A|} \begin{bmatrix} A_11 & A_12 & A_13 \\ A_21 & A_22 & A_23 \\ A_31 & A_32 & A_33 \\ \end{bmatrix} $$

Where,
A11,A12,...,A33 = Cofactors of A.
A = Mode or Determinant of A

Matrix Determinant Formula

The determinant of a square matrix A=aij of order 2 is the difference of product of its corresponding entries. The formula is,

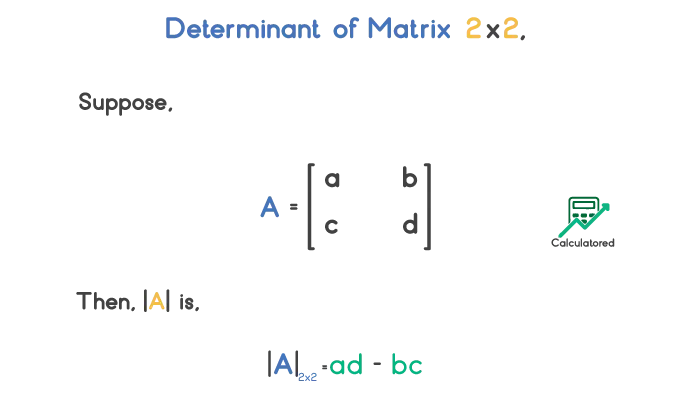
The determinant of a matrix A with order greater can be calculated by expanding it with its one row or column. That is,

Matrix Equation

An equation of the form Ax=B can be written in a matrix form of order m-by-n, called matrix equation. For example,

$$ a_1x + a_2y \;=\; b_1 $$ $$ a_3x + a_4y \;=\; b_2 $$

These equations can be written as:

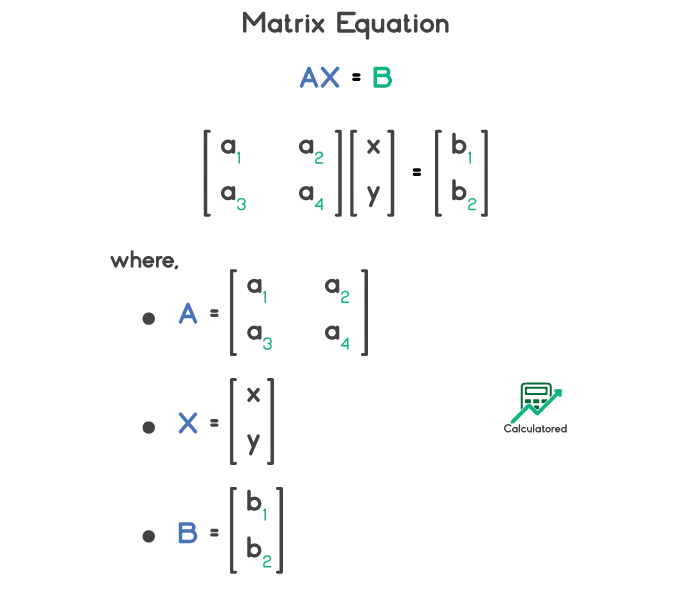
How do you Solve a Matrix?

The matrices are used to solve systems of linear equations. The basic operations on matrices are used to find their solutions. To find the inverse, determinant or adjoint of a matrix, you can use the following steps to solve the matrix equation.

• Write the system of linear equations in the matrix equation, such that,
$$ AX \;=\; B $$
• Write the matrix equation with all of its entries, such that,
$$ \begin{bmatrix} a_1 & a_2 \\ a_3 & a_4 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix} \;=\; \begin{bmatrix} b-1 \\ b_2 \\ \end{bmatrix} $$
• This equation can be solved by rearranging it such that,
$$ X \;=\; A^{-1}B $$
• Finding inverse of A matrix by using inverse formula.
• Substitute the solution of the inverse matrix in the matrix equation and find the product of the inverse of A with B.
• Solve simultaneously to find the solution of X.

FAQ’s

What are the applications of Matrix Formula?

Matrices have many applications not only in mathematics, they are widely used in science and engineering. In mathematics, matrices are used to solve systems of linear equations to find trivial and non-trivial solutions.

In graphic designing, digital images are referred to as matrices and the concept of rows and columns are equal to pixels. Moreover, in video gaming, matrices are helpful to convert 2D objects to 3D objects.

What is the Identity Matrix Formula?

The identity matrix formula for 2-by-2 and 3-by-3 order is,

$$ I \;=\; \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \;\; \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} $$

What is the Formula of Determinants?

The determinant of a matrix is calculated by the difference of product of its diagonal elements. The determinant formula for a matrix A is:

$$ A \;=\; \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \;\; and \;\; |A| \;=\; \begin{matrix} a & b \\ c & d \\ \end{matrix}$$ $$ |A| \;=\; ad-bc $$